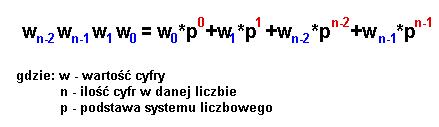17:00 <%Robol> siema all
17:00 <%Robol> jak wskazuje moj nick jestem Robol
17:00 <%Robol> ;]
17:00 <%Robol> mam na imie Piotrek
17:00 <%Robol> chodze do gimnazjum w Grybowie
17:00 <%Robol> jestem w III klasie
17:01 <%Robol> dzisiaj poprowadze wyklad n/t systemow liczbowych
17:01 <%Robol> no to zaczynamy
17:01 <%Robol> czlowiek od najdawniejszych czasow mial potrzebe liczenia
17:02 <%Robol> musial liczyc przedmioty ktore przenosil
17:02 <%Robol> i wtedy sobie wymyslil pierwszy system liczbowy
17:02 <%Robol> bylo to ok. 30000 lat p.n.e
17:03 <%Robol> polegal on na tym ze czlowiek zlobil sobie kreski na kosciach
17:03 <%Robol> np. III - to bylo 3
17:03 <%Robol> IIIIIIIII - to bylo 10
17:03 <%Robol> ten system pozniej ewoluowal
17:04 <%Robol> i czlowiek zaczynal oznaczac co 5 kreske jako taki ukosnik
17:04 <%Robol> czyli np. IIII\IIII\ - to bylo 10
17:04 <%Robol> pozniej ewolucja zrobila z niego cos takiego
17:04 <%Robol> IIII\IIIX
17:05 <%Robol> i to bylo nasze 10 ;]
17:05 <%Robol> podstawa systemu byla liczba 1
17:05 <%Robol> kolejnym systemem liczbowym jaki przedstawie byl rzymski

17:06 <%Robol> byl to wyeluowany system korbowy
17:06 <%Robol> ta obrazku jaki podalem mamy przyklady liczb
17:06 <%Robol> kolejne tworzylo sie przez ich dodawanie
17:07 <%Robol> Reguły zapisywania liczb w systemie rzymskim:
17:07 <%Robol> 1. Liczby zapisujemy jako sumę cyfr o następujących wartościach:
17:07 <%Robol> 2. Cyfry wypisujemy od strony lewej do prawej poczynając od największej.
17:07 <%Robol> 3. Jeśli przed cyfrą starszą stoi cyfra młodsza, to należy ją odjąć od starszej.
17:07 <%Robol> 4. Jeśli nad cyfrą umieszczono kreskę, to cyfra ta oznaczała liczbę tysięcy.
17:07 <%Robol> tym sposobem mozna bylo juz zapisywac bardzo duze liczby
17:07 <%Robol> rzymianie byli bardzo dumni ze swojego systemu
17:08 <%Robol> jednym z kolejnych systemow byl grecki
17:08 <%Robol> wymyslili go grecy ;P
17:08 <%Robol> byl on obarty na alfabecie greckim
17:09 <%Robol> ---ing---robol/2.jpg
17:09 <%Robol> liczby takze byly tworzone przez dodawanie do siebie odpowiednich liter

17:10 <%Robol> zeby napisac liczbe np. 1000 trzeba bylo dodac znak "ioty"
17:10 <%Robol> czyli taka kreske przed literka
17:10 <%Robol> wtedy literke sie mnozylo przez 1000
17:11 <%Robol> byl jeszcze symbol "miriady"
17:11 <%Robol> sluzyl on do mnozenia liczb przez 10000
17:11 <%Robol> pisalo sie duze M i nad tym liczbe
17:11 <%Robol> dobra, teraz system egipski

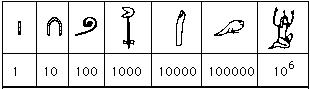
17:12 <%Robol> opieral sie on na obrazkach ktore oznaczaly kolejne potegi liczby 10
17:12 <%Robol> kolejne liczby otrzymywalo sie poprzez dodawanie do siebie rysonkow
17:13 <%Robol> zwrocmy uwage ze w tym alfabecie pojawila sie znowu liczba 10
17:13 <%Robol> jest to zwiazane z liczba naszych palcow
17:13 <%Robol> nasze paluczki byly naszym pierwszym przenosnym liczydlem
17:14 <%Robol> do dzis wielu ich uzywa do prostych obliczen ;]
17:14 <%Robol> dobra, teraz przechodzimy do pozycyjnych systemow liczbowych
17:15 <%Robol> pierwszym systemem pozycyjnym byl.... system korbowy
17:15 <%Robol> najpierw lepiej podam cechy systemow pozycyjnych ;]
17:15 <%Robol> Cechy zapisu pozycyjnego liczb
17:15 <%Robol> - ograniczona liczba cyfr, które posiadają poszczegolne wartosci 0,1,2,... Pomimo tego, system pozycyjny nie jest w zaden sposob ograniczony co do wielkosci zapisywanych liczb.
17:15 <%Robol> - podstawa systemu
17:15 <%Robol> - wartosc cyfry w zapisie zalezy od podstawy
17:15 <%Robol> - wartosc liczby w zapisie obliczamy jakosume iloczynow cyft przez wagi swoich pozycji

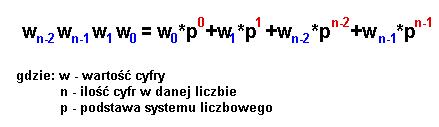
17:17 <%Robol> tutaj mamy wzor jak mozemy obliczyc wartosc liczby zapisanej w danym systemie
17:17 <%Robol> za chwile to wykorzystamy
17:17 <%Robol> no wiec liczby w systemie korbowym zapisywalismy w ten sposob
17:17 <%Robol> IIIIIIIIII
17:18 <%Robol> czyli 1*1^0+1*1^1+1*1^1+1*1^n
17:18 <%Robol> tym sposobem moglismy obliczyc wartosc
17:18 <%Robol> ale mozna inaczej
17:19 <%Robol> przeciez III+IIII=IIIIIII
17:19 <%Robol> nie trzeba zbednych obliczen
17:19 <%Robol> kolejnym systemem pozycyjnym byl system babilonski
17:20 <%Robol> byl to system o podstawie 60

17:20 <%Robol> uzywany jest do dnia dzisiejszego np. przy miezeniu czasu
17:20 <%Robol> powstal on w Mezopotamii
17:21 <%Robol> w tym systemie jako pierwszym wazna byla waga pozycji
17:21 <%Robol> do dyspozycji mielismy tylko takie dziwne kreski
17:22 <%Robol> pod koniec wykladu podam linka do strony gdzie jest dobrze wytlumaczone na czym ten system polegal i przyklady ;]
17:22 <%Robol> nastepnym systemem byl system Majow

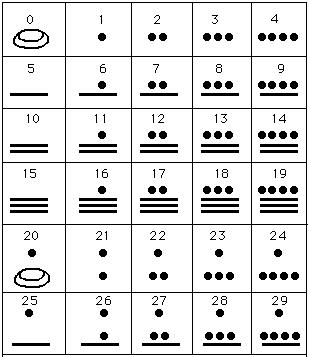
17:23 <%Robol> podstawa tego systemu byla liczba 20
17:23 <%Robol> przypuszczalnie dla tego ze majowie nosili sandaly i razem mozna bylo doliczyc sie 20 palcow
17:24 <%Robol> liczby w tym systemie skladaly sie z:
17:24 <%Robol> muszelki, oznaczala 0
17:24 <%Robol> kropki, oznaczala 1
17:24 <%Robol> i kreski czyli 5
17:25 <%Robol> w tym systemie jako pierwszym uzyto liczby 0
17:26 <%Robol> kolejnym i ostatnim systemem liczbowym byl i jest system arabski
17:26 <%Robol> jak sama nazwa wskazuje system pochodzil od hindusow ;P
17:28 <%Robol> Pierre-Simon Laplace (1749-1827), wielki matematyk francuski, napisał kiedys:
17:28 <%Robol> "Genialna metoda wyrazania kazdej mozliwej liczby przy uzyciu zbioru dziesięciu symboli (z których kazdy posiada wage pozycji oraz wartosc bezwzględna) wyłonila sie w Indiach. Dzisiaj pomysl ten wydaje się tak prostym, ix jego znaczenie i istota nie sajuz oceniane. Prostota tego pomysłu lezy w sposobie, w jaki ulatwia on wykonywanie obliczen, co umiesciło arytmetykę na czele uzytecznych wynalazkow, a znaczenie tego wynalazku może byc bardziej docenione, gdy z
17:28 <%Robol> \\ za ogonki sorki ale wklejalem ;]
17:29 <%Robol> tym systemem zajmiemy sie bardzo dokladnie
17:29 <%Robol> nasz system dziesiatkowy jak kazdy wie opiera sie na liczbie 10
17:30 <%Robol> czyli kolejna cyfra w liczbie jest kolejna potega liczby 10
17:30 <%Robol> wezmy sobie np. liczbe 164
17:30 <%Robol> mozna ja zapisac tak
17:30 <%Robol> 4*10^0+6*10^1+1*10^2
17:31 <%Robol> wiedziac juz cos takiego mozemy przekonwertowac liczby z kazdego systemu na 10
17:31 <%Robol> np liczba 11010011
17:31 <%Robol> obliczymy sobie tak:
17:32 <%Robol> 1*2^0+1*2^1+0*2^2+0*2^3+1*2^4+0*2^5+1*2^6+1*2^7
17:32 <%Robol> i liczymy ;]
17:33 <%Robol> 1+2+0+0+16+0+64+128
17:33 <%Robol> czyli 211
17:34 <%Robol> czyli sie zgadza ;]
17:34 <%Robol> tym sposobem mozemy juz sobie napisac proga ktory konwertuje liczby z innych systemow na 10, ale...
17:34 <%Robol> jest jeden problem
17:35 <%Robol> kazdy wie, i nawet dziadek wie (zakala rodzinna) ;]
17:35 <%Robol> ze komputer slabo poteguje
17:35 <%Robol> coz wiec robic
17:35 <%Robol> trzeba posluzyc sie innym algorytmem
17:36 <%Robol> Algorytm Hornera obliczania wartosci liczby calkowitej
17:36 <%Robol> n - liczba cyfr w zapisie pozycyjnym danej liczby
17:36 <%Robol> p - podstawa systemu pozycyjnego, w ktorym jest zapisana liczba
17:36 <%Robol> ci - cyfra stojąca na i-tej pozycji. Pozycja o numerze 0 jest pierwsza pozycja od strony prawej.
17:36 <%Robol> w - obliczana wartosc liczby
17:36 <%Robol> -------
17:36 <%Robol> w = 0
17:36 <%Robol> i = n - 1
17:36 <%Robol> w = ci + w x p
17:36 <%Robol> jeśli i = 0, to koniec, w zawiera wartosc liczby
17:36 <%Robol> i = i - 1
17:36 <%Robol> wroc do punktu 3
17:37 <%Robol> dzieki modyfikacjom naszego poprzedniego wzoru wg. wzkazowek zawartych w algorytmie Hornera wyszedl nam taki algorytm
17:37 <%Robol> nie wnikam juz jak to wyszlo ;]
17:38 <%Robol> i liczbe 11010011 sobie znowu przekonwertujemy wg niego
17:38 <%Robol> czyli
17:38 <%Robol> w=0
17:38 <%Robol> w=1+0x2=1
17:39 <%Robol> w=1+1*2=3
17:39 <%Robol> w=0+3*2=6
17:40 <%Robol> w=1+6*2=13
17:40 <%Robol> w=0+13*2=26
17:40 <%Robol> w=0+26*2=52
17:40 <%Robol> w=1+52*2=105
17:41 <%Robol> w=1+105*2=211
17:41 <%Robol> i wyszlo
17:42 <%Robol> teraz przejdziemy do liczb staloprzecinkowych
17:42 <%Robol> naszym starym algorytmem tez mozemy je konwertowac
17:42 <%Robol> przyklad: 1011,101
17:43 <%Robol> albo krotsza 101,01 ;] za duzo liczenia
17:43 <%Robol> no wiec tak:
17:45 <%Robol> 1*1^-2+1*0^-1+1*1^0+0*1^1+1*1^2
17:45 <%Robol> czyli to bedzie tak
17:47 <%Robol> no dobra to sobie sami obliczycie ;]
17:47 <%Robol> teraz wezmiemy znowu algorytm Hornera
17:48 <%Robol> tyle ze tym razem trzeba go ciut zmodyfikowac
17:49 <%Robol> Algorytm Hornera obliczania wartosci liczby stałoprzecinkowej
17:49 <%Robol> m - liczba cyfr po przecinku w zapisie pozycyjnym danej liczby
17:49 <%Robol> p - podstawa systemu pozycyjnego, w ktorym jest zapisana liczba
17:49 <%Robol> ci - cyfra stojąca na i-tej pozycji. Pozycja o numerze -m jest pierwszą pozycją od strony prawej.
17:49 <%Robol> w - obliczana wartosc liczby
17:49 <%Robol> w = 0
17:49 <%Robol> i = -m
17:49 <%Robol> w = (ci + w) / p
17:49 <%Robol> i = i + 1
17:49 <%Robol> jesli i = 0, to koniec, w zawiera wartosc liczby
17:49 <%Robol> w przeciwnym razie wroc do punktu 3
17:49 <%Robol> i znowu mamy liczbe 101,01
17:49 <%Robol> czyli robimy tak
17:49 <%Robol> w=0
17:49 <%Robol> w=1+0*2=1
17:50 <%Robol> w=0+1*2=2
17:50 <%Robol> w=1+2*2=5
17:50 <%Robol> taraz to po przecinku
17:51 <%Robol> w=0
17:51 <%Robol> w=(1+0)/8=1/8
17:52 <%Robol> sory w=(1+0)/2=1/2
17:52 <%Robol> w=(0+1/2)/2=1/4
17:52 <%Robol> czyli nasza liczba to 5 i 1/4
17:52 <%Robol> czyli 5,25
17:53 <%Robol> ale znowu mamy niedogodnosc
17:53 <%Robol> przy pisaniu programu bedziemy musieli zmieniac kolejnosc podawania cyfr
17:54 <%Robol> z pomoca przychodzi kolejny alg
17:54 <%Robol> Zmodyfikowany algorytm Hornera obliczania wartosci liczby stałoprzecinkowej
17:54 <%Robol> n - liczba cyfr w częsci całkowitej
17:54 <%Robol> m - liczba cyfr w częsci ułamkowej
17:54 <%Robol> p - podstawa systemu pozycyjnego, w ktorym jest zapisana liczba
17:54 <%Robol> ci - cyfra stojaca na i-tej pozycji. Pozycja o numerze 0 jest pierwsza pozycja od strony prawej.
17:54 <%Robol> w - obliczana wartosc liczby
17:54 <%Robol> w = 0
17:54 <%Robol> i = n - 1
17:54 <%Robol> w = ci + w x p
17:54 <%Robol> jesli i = -m, to w = w x p-m i kończymy
17:54 <%Robol> i = i - 1
17:54 <%Robol> wroc do punktu 3
17:55 <%Robol> w=1+0*2=1
17:56 <%Robol> w=0+1*2=2
17:56 <%Robol> w=1+2*2=5
17:57 <%Robol> w=0+5*2=10
17:57 <%Robol> w=1+10*2=21
17:58 <%Robol> 21*1/4=5,25
17:58 <%Robol> 21 to jest wynik
17:58 <%Robol> 1/4 to jest 1 podzielone przez droga potege liczby 2
17:59 <%Robol> dla tego 2 potega poniewaz mielismy 2 liczby po przecinku
17:59 <%Robol> no dobra teraz na odwrot
17:59 <%Robol> bedziemy zamieniac z 10 na binarny
18:00 <%Robol> wezmiemy sobie liczbe np. 58 ;]
18:00 <%Robol> 58/2=29 r. 0
18:00 <%Robol> 29/2=14 r. 1
18:00 <%Robol> 14/2=7 r.0
18:01 <%Robol> 7/2=3 r. 1
18:01 <%Robol> 3/2=1 r.1
18:01 <%Robol> 1/2=0 r. 1
18:01 <%Robol> odwracamy wszystkie reszty
18:01 <%Robol> i wychodzi nam liczba 111010
18:03 <%Robol> jezeli chcemy zmienic liczbe zmiennoprzecinkowa to trzeba zrobic inaczej
18:03 <%Robol> przykladowo mamy liczbe 24,2
18:03 <%Robol> czyli 24 i 2/10
18:04 <%Robol> 2/10 nalezy pomnozyc przez podstawe systemu do ktorego konwertujemy podniesiona do odp. potegi
18:06 <%Robol> wezmy sobie inny przyklad, z tym bedzie bardzo duzo liczenie ;]
18:06 <%Robol> np. 24,5
18:06 <%Robol> wtedy 5/10 mnozymy razy 2^1 czyli *2
18:07 <%Robol> (24,5)*2=49
18:07 <%Robol> i teraz to konwertujemy na bin
18:07 <%Robol> czyli
18:07 <%Robol> 49/2=24 r.1
18:07 <%Robol> 24/2=12 r.0
18:08 <%Robol> 12/2=6 r.0
18:08 <%Robol> 6/2=3 r.0
18:08 <%Robol> 3/2=1 r.1
18:08 <%Robol> 1/2=0 r. 1
18:08 <%Robol> mamy liczbe 110001
18:09 <%Robol> wczesniej dalismy *2^1 a wiec teraz trzeba dac przecinek w 1 miejsce przed od prawej
18:09 <%Robol> czyli 11000,1
18:10 <%Robol> moze teraz pytanka
18:10 <%Robol> wszyscy smacznie chrapia ;]
18:10 < fr3|code|off> chyba nie ma <:
18:10 < fr3|code|off> ale przygotowales sie widze <:
18:10 < oshogbo> zgubilem sie przy systemi binarnym
18:11 < oshogbo> znaczy sie zdrzemnolem ;)
18:11 <%Robol> ;]
18:11 < oshogbo> ale pozatym wykald bardzo cooooooooooooooooooooooooooooooooooooooool
18:11 <%Robol> no to jak masz problem to wal tylko nie za mocno
18:11 < fr3|code|off> pytanie tylko co
18:11 <%Robol> no dobra, no to gramy dalej
18:12 <%Robol> teraz moze przejzymy zapis zmiennoprzecinkowy
18:12 <%Robol> polega on na tym ze mamy matynse i wykladnik
18:12 <%Robol> mamy jeden fajny wzor
18:13 <%Robol> w=m*p^e
18:13 <%Robol> czyli wartosc=matynsa*podstawa systemu^wykladnik potegowy
18:13 <%Robol> i teraz przykladzik
18:14 <%Robol> mamy liczbe 542000000000000000 w systemie np. osemkowym
18:15 <%Robol> i teraz ten zapis mozemy sobie skrocic do postaci 0,542*8^18
18:16 <%Robol> to byl taki przyklad zamiany liczby staloprzecinkowej na zmiennoprzcinkowa, czy jak to tam sie zwie
18:16 <%Robol> podobno przydatne ;]
18:17 <%Robol> moze teraz sobie powiemy o zaleznosciach systemu binarnego
18:17 <%Robol> zobaczmy na przyklad 1111111
18:17 <%Robol> nie bede tego liczyl bo by bylo bardzo dlugo
18:18 <%Robol> wystarczy ze policze cyfry
18:18 <%Robol> jest ich 7
18:18 <%Robol> 2^7 jest 128
18:19 <%Robol> a zeby to bylo 2^7 to musiala by ta liczba miec 8 cyfr
18:19 <%Robol> i wygladala by tak
18:19 <%Robol> 10000000
18:19 <%Robol> a wiec nasza liczba jest o 1 mniejsza
18:19 <%Robol> wiec bardzo prawdopodobne ze to jest liczba 127 ;]
18:20 <%Robol> i teraz dam wam ciekawa rzecz do zapamietania
18:21 <%Robol> Na n bitach mozna zapisac w naturalnym kodzie binarnym liczby z przedziału:
18:21 <%Robol> (0, 2^(n - 1))
18:22 <%Robol> no dobra to teraz moze co mozemy robic z systemem binarnym
18:22 <%Robol> oczywiscie mozemy dodawac
18:22 <%Robol> wystarczy znac tabliczke dodawania w systemie binarnym
18:23 <%Robol> oto ona:
18:23 <%Robol> Tabliczka dodawania
18:23 <%Robol> 0 + 0 = 0
18:23 <%Robol> 0 + 1 = 1
18:23 <%Robol> 1 + 0 = 1
18:23 <%Robol> 1 + 1 = 10
18:23 <%Robol> i teraz mozemy sobie dodawac liczby
18:23 <%Robol> wezmy sobie np. 1100 i 1001
18:23 <%Robol> 1100
18:23 <%Robol> 1001
18:23 <%Robol> ----
18:23 <%Robol> 10101
18:24 <%Robol> czyli po przekonwertowaniu wyjdzie
18:24 <%Robol> 12+9=21
18:24 <%Robol> a wiec dziala ;]
18:25 <%Robol> teraz mnozenie
18:25 <%Robol> nie jest to takie trodne
18:25 <%Robol> IMHO jest nawet prostsze od tego dziesiatkowego
18:25 <%Robol> Tabliczka mnozenia
18:25 <%Robol> 0 x 0 = 0
18:25 <%Robol> 0 x 1 = 0
18:25 <%Robol> 1 x 0 = 0
18:25 <%Robol> 1 x 1 = 1
18:25 <%Robol> teraz sobie pomnozymy wczesniejsze liczby
18:26 <%Robol> 1100
18:26 <%Robol> 1001
18:26 <%Robol> ----
18:26 <%Robol> 1100
18:26 <%Robol> 0000
18:26 <%Robol> 0000
18:26 <%Robol> 1100
18:27 <%Robol> kazde kolejne mnozenie w dzialaniu powinno byc przesuniete o pozycje w lewo ale z powodow technicznych...
18:27 <%Robol> teraz dodajemy sobie liczby
18:27 <%Robol> i wychodzi...
18:28 <%Robol> 1101100
18:28 <%Robol> czyli 12*9=108
18:29 <%Robol> to prawda, wiec sie udalo
18:29 <%Robol> oczywiscie mozna sprobowac z dzieleniem i odejmowaniem ale nie bedziemy juz tego tutaj przerabiac
18:30 <%Robol> *ReWolf* 1100
18:30 <%Robol> *ReWolf* 1001
18:30 <%Robol> *ReWolf* ----
18:30 <%Robol> *ReWolf* 1100
18:30 <%Robol> *ReWolf* 0000
18:30 <%Robol> *ReWolf* 0000
18:30 <%Robol> *ReWolf* 1100
18:30 <%Robol> *ReWolf* -------
18:30 <%Robol> *ReWolf* 1101100
18:31 <%Robol> ;]
18:31 <%Robol> no dobra
18:31 <%Robol> teraz przejdziemy do konwersji dwojkowo - osemkowej
18:32 <%Robol> kazdy wie i nawet dziadek wie, ale zapomina
18:32 <%Robol> ze 8=2^3
18:33 <%Robol> a wiec mozna zapisac liczby binarne w postaci osemkowych bez zadnych problemow
18:33 <%Robol> cyfry osemkowe
18:33 <%Robol> cyfra wartość
18:33 <%Robol> 0 000
18:33 <%Robol> 1 001
18:33 <%Robol> 2 010
18:33 <%Robol> 3 011
18:33 <%Robol> 4 100
18:33 <%Robol> 5 101
18:33 <%Robol> 6 110
18:33 <%Robol> 7 111
18:34 <%Robol> i teraz mozemy sobie konwertowac
18:34 <%Robol> przykladowo mamy liczbe...
18:34 <%Robol> 110 001 010 110 100
18:34 <%Robol> i sobie ja konwertujemy na osemkowy
18:35 <%Robol> czyli wyjdzie nam takie cos...
18:35 <%Robol> 110 001 010 110 100
18:35 <%Robol> 6 1 2 6 4
18:36 <%Robol> i mamy liczbe 61264 zapisana w systemie oct czyli osemkowym
18:36 <%Robol> tak samo mozemy zamieniac na odwrot
18:37 <%Robol> np. liczba 170 to bedzie 001 111 000
18:37 <%Robol> no dobra
18:37 <%Robol> i znowu dziadek wie... ze 16=2^4
18:38 <%Robol> czyli rownie prosto mozemy sobie konwertowac z hex do bin
18:38 <%Robol> cyfry szesnastkowe
18:38 <%Robol> cyfra wartosc
18:38 <%Robol> 0 0000
18:38 <%Robol> 1 0001
18:38 <%Robol> 2 0010
18:38 <%Robol> 3 0011
18:38 <%Robol> 4 0100
18:38 <%Robol> 5 0101
18:38 <%Robol> 6 0110
18:38 <%Robol> 7 0111
18:38 <%Robol> 8 1000
18:38 <%Robol> 9 1001
18:38 <%Robol> A 1010
18:38 <%Robol> B 1011
18:38 <%Robol> C 1100
18:38 <%Robol> D 1101
18:38 <%Robol> E 1110
18:38 <%Robol> F 1111
18:39 <%Robol> no i teraz mamy sobie cyfre np. A53F
18:39 <%Robol> i sobie ja konwertujemy
18:40 <%Robol> A 5 3 F
18:40 <%Robol> 1010 0101 0011 1111
18:40 <%Robol> o cholera
18:40 <%Robol> jeszcze zostalo kodowanie liczb dwojkowych ze znakiem
18:40 <%Robol> trza szybko przejsc
18:41 <%Robol> no to 1. sposob
18:41 <%Robol> kod znak-modol
18:41 <%Robol> czyli np. 1101
18:41 <%Robol> to bedzie -5
18:41 <%Robol> a dlaczego?
18:42 <%Robol> bo teraz sie tak umowilismy ze bedziemy sobie kodowac takze znak
18:42 <%Robol> i w systemie znak-modol pierwsza cyfra zawsze oznacza znak
18:42 <%Robol> 1 - minus
18:42 <%Robol> 0 - bez znaku
18:43 <%Robol> i taraz co sprytniejsi zauwazyli ze 1000 i 0000 to ta sama liczba, czyli zero
18:43 <%Robol> ano tak
18:43 <%Robol> bo w tym systemie mozemy zakodowac liczby od 127 - -127
18:43 <%Robol> taki system ;\
18:43 <%Robol> no i 2. sposob
18:43 <%Robol> kod U2
18:44 <%Robol> w tym kodzie pierwsza cyfra w liczbie jest zawsze ujemna
18:45 <%Robol> czyli liczba 1101 to bedzie -2^3+1^2+0^1+1^0
18:45 <%Robol> i tym sposobem 1101 bedzie oznaczalo 8-5 czyli -3
18:46 <%Robol> w tym systemie nie ma tego bledu co w poprzednim czyli, mozna zapisac liczby od 127 - -128
18:46 <%Robol> wiec jest lepszy
18:47 <%Robol> na kodzie U2 mozemy takze wykonywac dzialania np. dodawanie, etc.
18:47 <%Robol> ktore na kodzie znak-modol byly niedopuszczalne
18:47 <%Robol> i jeszcze ostatnia ciekawostka dotyczaca kodu U2
18:48 <%Robol> aby znalezc wartosc przeciwna w kodzie U2 nalezy wykonac następujace czynnosci:
18:48 <%Robol> - zamienic wszystkie bity liczby na przeciwne, tzn. 1 na 0 i 0 na 1
18:48 <%Robol> - do tak otrzymanej liczby dodac wartość 1
18:48 <%Robol> czyli jezeli mamy liczbe 7
18:48 <%Robol> czyli 111b
18:49 <%Robol> to zamieniamy jedynki na zera
18:49 <%Robol> czyli 0000
18:49 <%Robol> zle podalem
18:49 <%Robol> 0111b - teraz dobrze
18:49 <%Robol> zamieniamy i mamy 1000b
18:50 <%Robol> dodajemy 1
18:50 <%Robol> i wychodzi 1001 czyli -7
18:50 <%Robol> to by bylo na tyle
18:50 <%Robol> pytania?
18:50 <%Robol> co to jest to b na koncu?
18:50 <%Robol> b czyli liczba zapisana w systemie binarnym
18:51 <%Robol> tak samo o oznacza oct czyli system osemkowy
18:51 <%Robol> h oznacza hex czyli 16
18:51 <%Robol> liczby w systemie 16 mozemy zapisac jeszcze dodajac przed nimi 0x
18:51 <%Robol> czyli np. liczba 84Ah = 0x84A
18:52 <%Robol> i to by bylo na tyle ;P