W poprzednim poście pisałem o narzędziu do pomiaru entropii, natomiast kwestię "po co komu pomiar entropii" zostawiłem wtedy na któryś kolejny post. Czas ów postu właśnie nadszedł.

Jak czytelnik może się domyślić (patrząc na otagowanie tego postu) pomiar entropii może przydać, w fazie rekonesansu, się osobom zajmującym się reverse engineering'iem. Dzięki pomiarowi entropii można wskazać w pliku miejsca gdzie występują pewne anomalie związane z szyfrowaniem kodu/danych, z pustym miejscem w pliku, występowaniem danych skompresowanych, tekstowych, bitmap, etc.

Zacznijmy od początku, czyli - czym jest entropia (w kontekście informatycznym, nie fizyczny, chociaż to się wiąże)? Osobiście bardzo lubię nieformalną definicję mówiącą że entropia jest miarą chaosu, czyli, czym dane są bardziej chaotyczne/losowe, tym ich entropia jest wyższa, natomiast jeżeli dane są "monotonne", uporządkowane, nielosowe, tym entropia niższa. Dowiedzieliśmy się dwóch rzeczy: (1) entropia to miara losowości (2) pewnej partii danych. W naszym, związanym z RE, przypadku, możemy uściślić iż 'partia danych' odnosi się do konkretnej ilości kolejnych bajtów w pliku / pamięci / pakiecie sieciowym / etc. Jeszcze bardziej uściślając, w przypadku Ent'a jedna partia danych to 256 kolejnych bajtów.

Jak wyliczyć entropię? Metod jest tak na prawdę kilka. Metoda którą ja używam jest trochę uproszczona (tj. nie wyłapuje wszystkich korelacji), i polega na analizie histogramu (czyli tablicy częstości występowania każdego 'rodzaju' bajtu - np. 'A' występuje 100 razy, 'B' 50, etc) w partii danych - taki histogram ma oczywiście 256 wpisów (bo jeden bajt może przyjąć 256 różnych wartości). Następnie, dla każdego wpisu w histogramie, wykonuje Entropia += Ilość_Wystąpień[X]^2 / Ilość_Danych, gdzie X są kolejne wartości bajtów (od 00 do FF) (na koniec możemy jeszcze entropie podzielić przez wielkość próbki danych, i odwrócić wartość (X = 1-X), wg własnego uznania, ja tak robie). Dobrym pomysłem jest również wyliczenie E^2 (entropii do kwadratu), wtedy wartości są bardziej "czytelne" - będę E^2 oznaczał jako E".

Przykładowo, weźmy następujący fragment 50 bajtów:

ABCABCCABCABACBABABABABABABCABACBACBABABACBABACBAB

Następnie stwórzmy histogram:

A - 20
B - 20
C - 10
inne - 0

Po czym wyliczmy entropię (E):

E = 0                (    E = 0   )
E += 20 * 20 / 50    ('A' E = 8   )
E += 20 * 20 / 50    ('B' E = 16  )
E += 10 * 10 / 50    ('C' E = 18  )
E = 1 - (E / 50)     (    E = 0.64)
E" = E^2             ( E" = 0.4096)

Czyli końcowa entropia tego fragmentu wynosi 0.64, czy tam 64%, a E" 40,96%. Od tego momentu będziemy używać jedynie E", tak żeby się nie mieszało.

Żebyśmy mieli rozeznanie co to znaczy 40%, policzmy E" dla dwóch innych ciągów (podam od razu wyniki):

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA - E" = 0.00%
ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwx - E" = 96.04%

Czyli jak widać same literki A mają zerową entropię, natomiast ciąg w którym każda możliwa wartość bajtu występuje tylko raz ma entropie 96.04%. No Właśnie, czemu 96.04% a nie 100%? Tak niestety wynika z trochę upośledzonego zastosowania wzoru - czym większa jest partia danych tym bardziej do 100% maksymalna entropia może się zbliżyć. Tak na prawdę maksymalna wartość E wynosi (1 - (1 / Ilość_Danych)), i wypadało by przeskalować E do skali 0 - 100%, czyli pomnożyć E przez 1 / (1 - 1/Ilość_Danych), ale tak na prawdę do jest to mało istotne.

A co nam daje taka miara losowości? Otóż okazuje się że różne "rodzaje" danych mają różną entropię. Kilka prawidłowości które udało mi się stwierdzić (dla danych wielkości 256 bajtów):
1) Dane/kod zaszyfrowane "nieprostym" szyfrem (definicje "nieprostego" szyfru podam niżej) mają E" >= 97%
2) Dane/kod skompresowane mają E" >= 97%
3) "Puste" miejsca (np. wyzerowane dane) mają E" == 0%
4) Identyczne dane w kilku kolejnych fragmentach danych mają stałą (względem siebie) E"
5) Kod x86 ma 80% <= E" <= 95%
6) Dane tekstowe mają 18% <= E" <= 90%
7) Nagłówki mają zazwyczaj "bardzo niską" E" (z uwagi na sporą ilość zer występujących tu i tam), zazwyczaj na poziomie 50%
8) Dane losowe mają bardzo wysoką entropię, E" >= 97%
9) Klucze do szyfrów mają bardzo wysoką entropię, E" >= 97%
10) Tablice dla algorytmów typu AES czy MD5 mają bardzo wysoką entropię, E" zależne od kompilatora, zazwyczaj >= 92%

Małe wyjaśnienie co do "nieprostego" szyfru, na zasadzie kontrastu - "prosty" szyfr w tym wypadku, to taki szyfr który nie zmienia entropii, czyli zmienia bajty, ale nie zmienia wyglądu "posortowanego" histogramu, tj. jeżeli przed zaszyfrowaniem najczęściej występujący znak pojawiał się 100 razy, to po zaszyfrowaniu najczęściej występujący znak nadal będzie pojawiać się 100 razy, mimo iż będzie to inny znak. Przykładami takiego szyfru "prostego" są:
1) Dodanie STAŁEJ jedno-bajtowej liczby do każdego bajtu
2) Odjęcie STAŁEJ jedno-bajtowej liczby od każdego bajtu
3) XOR STAŁEJ jedno-bajtowej liczby z każdym bajtem
4) Obrót bitowy każdego bajtu w prawo lub w lewo o STAŁĄ ilość bitów
5) Inne dowolne przestawienie bitów w każdym bajcie wg STAŁEGO wzorca
6) Inna odwracalna operacja na każdym bajcie, identyczna dla każdego bajtu
7) Złożenia powyższych

Szyfry proste, z uwagi na zastosowany wzór, entropii nie zmienią. Natomiast każdy inny szyfr ZMIENI entropię - zazwyczaj znacznie ją zwiększając (pomijam jakieś ultra dziwne przypadki XORa w których klucz jest długości danych i powoduje powstanie ciągu identycznych bajtów - to zmniejszy entropię). Kilka przykładów szyfrów zmieniających entropię:
1) Dodanie do każdego bajtu jego pozycji
2) XOR z długim kluczem o niezerowej entropii
3) AES, RC4, etc

Czas na kilka obrazków (wygenerowanych przez Ent'a), wraz z omówieniem. Jeszcze taka mała uwaga - jeżeli chcemy się dowiedzieć gdzie dany Ent'owy 'słupek' leży w pliku, wystarczy wziąć pozycję X tego słupka, i pomnożyć ją przez 256 - np. słupek jest na X=83, więc dane są na HEX(83*256), czyli 5300h.


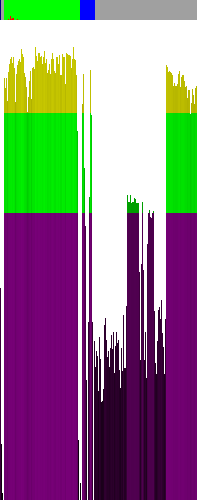
Powyższy wykres przedstawia entropię skompilowanej MinGW GCC, niestripniętej, wersji Ent'a. Kilka wniosków z niego:
1) Żadna część nie jest zaszyfrowana nieprostym szyfrem
2) Na samym początku znajdują się nagłówki, a po nich ponad 256 bajtów zer, lub innych stałych bajtów (patrz pierwsze 4ry kolumny)
3) W sekcji kodu (zielone oznaczenie na górze) znajduje się faktycznie kod ;>
4) W sekcji danych (niebieskie oznaczenie na górze) jest sporo zer, oraz dwie "partie" danych, być może tekstu (5300h oraz 5A00)
5) W "szarej strefie" znajduje się trochę nagłówków (niska entropia na samym środku obrazu) - nagłówki/informacje dla debuggera?
6) W "szarej strefie" mniej więcej od 125 do 152 piksela znajduje się trochę podniesiona (względem nagłówków) entropia, jakieś informacje tekstowe dla debuggera?
7) Po prawej stronie obrazu znajduje się sporo wysokiej entropii, skoro to nie kod, to prawdopodobnie są to dane tekstowe (są tam nazwy symboli)


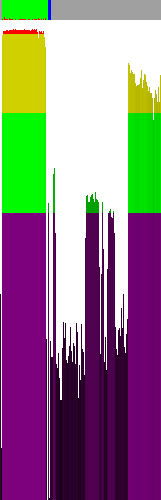
Ten sam plik, spakowany UPXem. Kilka wniosków:
1) Sekcja kodu jest zaszyfrowana lub skompresowana
2) Na końcu sekcji kodu (2-3 ostatnie słupki) jest trochę niezaszyfrowanego kodu (w rzeczywistości jest tam loader dekompresujący)
3) Reszta wniosków jak w poprzednim przypadku


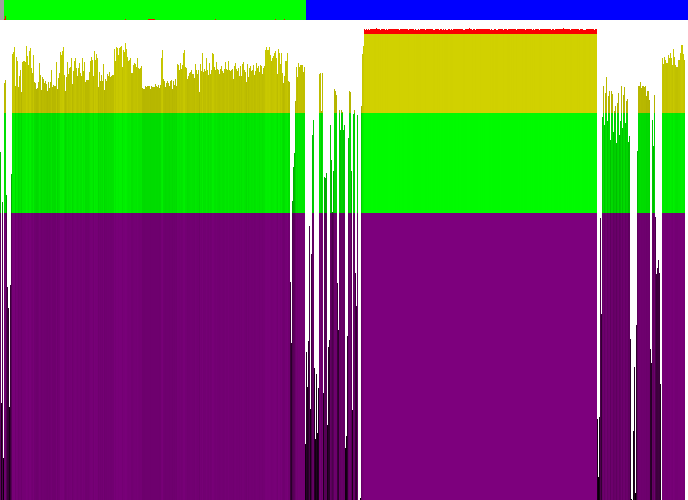
Kalkulator z Visty. Wnioski:
1) Nagłówków jest dość sporo przed sekcją kodu
2) Sekcja kodu nie jest zaszyfrowana ani skompresowana
3) W sekcji kodu w okolicy 291 piksela (12300h) jest znaczne obniżenie entropii, prawdopodobnie jest to IAT, po którym następują (znowu wysoka entropia) nazwy importowanych funkcji (trudno o inne wyjaśnienie tego fenomenu)
4) Duża część danych jest skompresowana lub zaszyfrowana (tak na prawdę znajduje się tam plik PNG 256x256x32 przedstawiający kalkulator)
5) Pod koniec pliku znajdują się prawdopodobnie znowu jakieś nagłówki i trochę tekstu
6) Z uwagi na rodzaj aplikacji, prawdopodobnie większość sekcji niebieskiej to zasoby (ikonki, dialogi, takie tam)


Jakiś spakowany PEncrypt 3.1 malware (downloader):
1) Pierwsza sekcja z kodem jest szyfrowana lub skompresowana
2) Druga sekcja z kodem nie jest zaszyfrowana, zawiera prawdopodobnie loader
3) Sekcja danych jest niezaszyfrowana


Program z Hackerchallenge 2008 Phase 3:
1) Trzy różne części sekcji kodu są zaszyfrowane, prawdopodobnie oddzielnie
2) Sekcja danych jest zaszyfrowana LUB (z uwagi na bardzo równą entropie tego fragmentu) znajdują się tam klucze lub tablice stałych dla jakiegoś algorytmu szyfrującego (klucze + stałe dla AES tam były afair)
3) Na końcu pliku znajduje się jakiś stały padding (wyjątkowo równa entropia, jakiś ciąg XPADDINGX powtarzający się masę razy tam jest)

By the way...
On 22nd Nov'24 we're running a webinar called "CVEs of SSH" – it's free, but requires sign up: https://hexarcana.ch/workshops/cves-of-ssh (Dan from HexArcana is the speaker).

To na tyle galerii. Na koniec powiem tylko że korzystam z wykresów entropii od jakiś dwóch lat w pracy, i bardzo przyspieszył analizę paru rzeczy, głównie dlatego że jeden rzut oka na wykres pozwala stwierdzić (z dużym prawdopodobieństwem):
1) czy plik jest zaszyfrowany
2) gdzie znajdują się zaszyfrowane części
3) gdzie znajduje się tekst
4) jak mniej więcej jest rozłożony tekst
A to daje całkiem niezłego boosta już na samym początku analizy ;>