A few days ago I had a fun chat with Ange Albertini about secure design of file formats – a topic Ange has been passionately researching for some time now. One of the specific problems that we discussed were overlarge fields and how to approach them in a file format or communication protocol design in a way that makes certain that their handling is safe and secure by default. In this blogpost I wanted to discuss two of my ideas (neither of which is perfect) and related observations on this topic.

What is an overlarge field?

It's best to explain this using one of my favorite examples – same one I've used in my "How to find vulnerabilities?" blog post and in several talks.

In the GIF image format specification there is a field called LZW code size which holds the initial LZW compression code size in bits.

         7 6 5 4 3 2 1 0
        +---------------+
        | LZW code size |
        +---------------+

What exactly the value entails isn't really important for this discussion. What is however important is that said value must be between 3 and 12 (inclusive).

The second important piece of information is that the field holding this value is a typical byte (8-bit) field.

This of course means that while on paper the value should be between 3 and 12, technically the actual field in a GIF file can contain any value in the range of 0 to 255. I.e. the field is too large for the actual value it's supposed to hold and thus I call it an overlarge field¹.
¹ Do note that this isn't an official term, just something I'm going to use for the sake of this blog post.

The problem with overlarge fields

I'm pretty sure that for any vulnerability researcher the previous section just screams "buffer overflow!". To be more precise, before a value read from this field can be safely used, it needs to be run through a validation check like this (pseudocode):

While this code is rather trivial and not unlike a hundred other checks in a parser, there are two problems with it:

1. A programmer can forget / neglect to add it and in doing so introduce a buffer overflow vulnerability (e.g. CVE-2009-1098).
2. A programmer needs to spend energy to securely handle this field, meaning it's insecure by default, as if they would not spend the required energy the code would be (or rather would remain) vulnerable.

Do note that this problem is pretty typical for "quantity" values stored in overlarge fields as they tend to be used without any kind of mapping or translation in further buffer size/indexing-related calculations. It's not so bad for e.g. enumerated type values, as these tend to be used in a switch-case construct which usually handles any unexpected values in a default: statement (unless one forgets that as well of course; yet still the consequences are usually less dire... I think?).

So if we would be designing a new binary file format or a new binary protocol, how could we address this issue?

Overlarge fields secure by default

The main requirement is the following: the field should be designed in a secure-by-default way, meaning that if a programmer does nothing (i.e. doesn't spend any additional energy) it's unlikely that a vulnerability would be introduced.

The following sub-sections contain two ideas I came up with.

Simple mapping

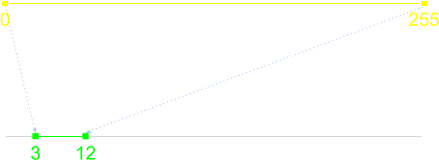
The initial idea I had was to use a mathematical function that performs full mapping of the one range into the other. For our example byte field value of [0, 255] could be fully mapped to actual value of [3, 12] by using a simple scaling and translation function like this one:

By using this method we make sure that no value that is read from the byte field would result in an invalid value (i.e. there is no need to write any range checking). At the same time this function isn't really something that a programmer could accidentally or purposefully skip during implementation, as any test samples would likely break indicating an issue.

On the flip side there are three potential downsides to this solution. First of all most actual values can be encoded in several different ways. For example, actual value 7 can be encoded using 114 as well as 141, or any number in between. There are two consequences of this: it opens the format to steganography (though this might be considered a feature) and it makes creating signatures harder (example: an exploit was observed in the wild and it has been established that it needs to have the byte field value set to 114, thus a signature was created to look for byte field value of 114; an attacker can just tweak the 114 to e.g. 115 to get the same actual value while evading detection).

Secondly, the math, while simple, might be a bit more tricky to implement on 8-bit platforms or platforms with no IEEE-754 floating points. Any rounding inconsistencies between platforms might also result in discrepancies (e.g. value 141 being mapped to 7 on one platform, but to 8 on another). In general It Should Be Fine™, but I'm pretty sure there would be a weird platform somewhere where this would cause issues for programmers.

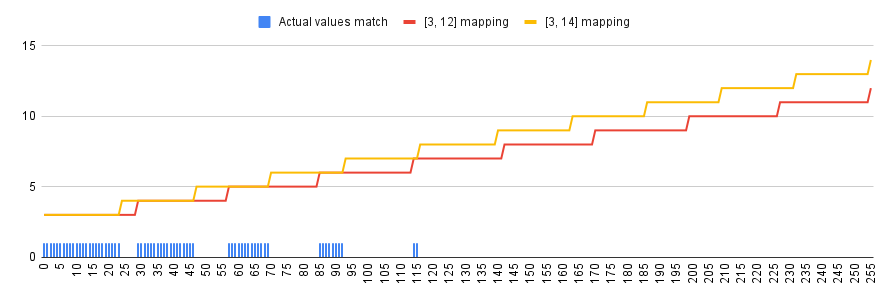
Another interesting issue might come up if the format/protocol gets a new version in which the given field's range of actual values would change from [3, 12] to e.g. [3, 14] (resulting in the scaling factor change). An old parser which would neglect to do a proper version check would map "new" byte values into the "old" actual value range (i.e. use incorrect scaling factor). Depending on the specifics this might even go undetected if tests don't cover the whole range of values. In our example 65 out of 256 byte values do result in correct actual values due to the overlap of output (refer to the chart above). It would likely not be a huge problem, but might result in a parser that "sometimes works, sometimes doesn't, no one knows why" (until properly debugged of course).

One more thing to add: it might be tempting to just use the % modulo operand here (e.g. actual_value = byte_value % 13) – same as one uses for pseudo-random numbers – instead of a scaling function. The issue with modulo however is that if one forgets it, things will very likely still work since well formed test samples will likely contain only values from the primary range. This is bad, as the the issue will not be caught and the code will be shipped with a potential security bug.

Unique random value mapping

Thinking on the previous solution I came to the conclusion that the culprit there is that math function. So how about we go the other way – i.e. make sure that there is no "simple mathematical function" mapping between byte field values and actual values? This can be achieve by creating a 1-to-1 mapping between unique semi-random values and actual values. Here's an example:

This of course is a bit more annoying to implement (reformatting tables of values into the desired form). It also will work only for small ranges. It's fine for a table of 10 values, but it's just impractical for e.g. 1 million values; not to mention that it would exceed the flash capacity of some 8-bit devices and in general bloat up the parser.

One other potential issue here is what would the parser do in case of dealing with a value that's not in the translation table. The proper thing to do would be to immediately stop parsing and throw an exception. However the default thing that will happen – in case a programmer doesn't introduce any special handling – will be whatever the used lookup function does in such case. That's all good and well for Python which will throw a KeyError exception. But C++'s std::map or std::unordered_map would return 0 (assuming typical code like BYTE_VALUE_TO_ACTUAL_VALUE[byte_value]), which introduces the need for spending energy to make a pre-check. It's no longer secure-by-default. JavaScript is pretty close to C++, returning undefined both in case of a typical object and Map, which – unhandled – can cause all sorts of issues down the line (see for example the 16 snowmen attack by Daniel Bleichenbacher²).
² Apparently it's really hard to find a link to the original issue description, but here are two links that do describe it: slides 20-25, first half of this blog post.

Unique random values do help a bit with extending the field in the future (like that [0, 12] to [0, 14] extension mentioned as an example before), as both backward compatibility and breaking backward compatibility can be easily achieved. In the first case you keep the values you have and just add new ones (e.g. 0xab and 0x72 in our example). If you want to break compatibility however, you deprecate all previous values (i.e. remove them and not use them) and introduce new ones. I guess making the field a bit bigger (e.g. 2 or 4 bytes) would give one more room to maneuver if future changes need to be made, but at the same time this would increase the bloat and introduce a temptation on 8-bit platforms to check only 1 byte instead of all of them (which might not be future proof in case new unique values would be added that actually share that 1 specific byte).

By the way...
On 22nd Nov'24 we're running a webinar called "CVEs of SSH" – it's free, but requires sign up: https://hexarcana.ch/workshops/cves-of-ssh (Dan from HexArcana is the speaker).

Summary

Neither the simple mapping nor the unique random value mapping methods are perfect – in either case there are pros and cons. And it needs to be noted that both methods add a bit of complexity to the format/protocol – especially when one imagines that there are multiple such fields, each with their own mapping function or distinct mapping table. Still, it was a fun thought exercise.

I also need to note that I didn't research what has been written on this topic – perhaps someone devised a better solution which I just never heard of. If you have a link to something related, please let me know.