Niecałe pół roku temu stwierdziłem że przydała by mi się animowana tapetka, generowana realtime, ale bez użycia akceleracji 3D (tj. bez OpenGL/D3D). Dodatkowymi założeniami był FPS - mógł być bardzo niski, na poziomie 2-3 klatek na sekundę, oraz wykorzystanie kilku core'ów (do 4rech). Jak to w życiu bywa, naklepałem troszkę kodu, po czym zająłem się innymi rzeczami. Efekt może powalający nie wyszedł, ale zdecydowałem się i tak opisać to co mi wyszło - może kogoś to zainteresuje ;> (na obrazki, z wyjątkiem height mapy, można klikać; kod źródłowy dla Windowsa/Maca/Linuxa i filmik są na końcu postu).

Po lewej stronie znajduje się obrazek efektu końcowego (teren się nie przesuwa, tylko światła są przeliczane). Na wypadek gdyby ktoś nie domyślił się co to jest - jest to oświetlony fragment nieoteksturowanego terenu. Dodam że w obecnej wersji aplikacji kursor myszki jest źródłem światła (hmm... bardziej poprawnym będzie powiedzenie że kursor myszki jest powiązany ze źródłem światła ;D). OK, a teraz krótki ilustrowany opis jak doszło do takiego efektu.

Podstawą całości jest heightmapa wielkości 4097x4097 (po prawej jest jej miniaturka, pełna wersja dołączona jest do źródeł - 4097x4097x8 RAW; wielkość heightmapy wynika z rozdzielczości której używam na desktopie - 3200x1200 (2x1600x1200)), a do jej zaprezentowania w 3D została użyta dość zabawna technika polegająca na rysowaniu słupków o wysokości wynikającej z heightmapy, rozpoczynając od końca ekranu (tak żeby słupki się nakładały). Rysunek poniżej przedstawia koncepcyjnie jak taki proces wygląda.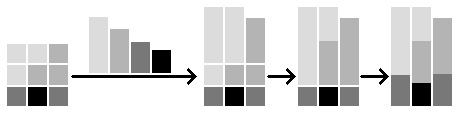

Jak widać, heightmapa jest odrobinę rozmyta w górnej części, i bardziej ostra w dolnej - miało to na celu zasymulowanie efektu zaniku części detali wraz ze zwiększającą się odległością. Taką transformację można spokojnie przerzucić do kodu (rozmycie Gaussa ze zmniejszającym się promieniem).

Heightmapa poddawana jest jeszcze jednej transformacji mającej na celu uzyskanie efektu perspektywy. Całość jest dość prosta - czym "dalej" tym mniejszy współczynnik przy obliczaniu wysokości słupka. W kodzie odbywa się to w funkcji MakePicture() za pomocą następującego kodu:

 for(z = 0; z < HMAP_DEPTH; z++)
 {
   float mody = powf((float)(1 + HMAP_DEPTH - z), 0.1);
   for(x = 0; x < HMAP_WIDTH; x++)
     hmap[x + z * HMAP_WIDTH] /= mody;
 }

Tablica hmap to oczywiście heightmapa. Do oznaczenia głębi użyłem 'z' a nie 'y'. HMAP_DEPTH i HMAP_WIDTH to wielkość heightmapy (4097). Bez nałożenia tej transformacji, teren wyglądał by tak jak na obrazku po lewej. Tak na prawdę współczynnik perspektywy jest w tym wypadku tylko i wyłącznie kwestią gustu, bo imho oba obrazki mają swój urok.

Kolejnym krokiem jest wyliczenie normali (wektorów wskazujących w którą stronę skierowana jest dana "ścianka" skały). Trochę tutaj oszukałem, i skorzystałem z wzoru na wyliczenie wektora normalnego dla trójkątów, tracąc tym samym część precyzji wynikającej z faktu że na jedną "ściankę" składają się 4 piksele (wierzchołki) a nie 2). Normale liczone są na podstawie heightmapy po nałożeniu perspektywy, i odpowiada za to następujący kod (wykonywany dla każdej ścianki, czyli dla każdego kwadratu o boku 2 z heightmapy, czyli de facto dla każdego punktu heightmapy):

 // Make a triangle
 float max_y_prev[3] = {
   hmap[(x - 0) + (z - 0) * HMAP_WIDTH],
   hmap[(x - 1) + (z - 0) * HMAP_WIDTH],
   hmap[(x - 0) + (z - 1) * HMAP_WIDTH]
 };
       
 Vector3D vp_all[3] = {
   Vector3D( (float)x, (float)max_y_prev[0], (float)z ),
   Vector3D( (float)(x-1), (float)max_y_prev[1], (float)z ),
   Vector3D( (float)x, (float)max_y_prev[2], (float)(z-1) )
 };
 
 // Calc normal for that triangle
 // XXX the correct way should have two triangles with some avg. normal, but who cares ;p
 PreNormalMap[x + z * HMAP_WIDTH] = calc_normal(vp_all);

 [...]
 
Vector3D calc_normal(Vector3D v[3])
{
 Vector3D out = Vector3D(0,0,0);
 Vector3D v1, v2;

 // Do some math
 v1 = v[0] - v[1];
 v2 = v[1] - v[2];

 out.x = v1.y*v2.z - v1.z*v2.y;
 out.y = v1.z*v2.x - v1.x*v2.z;
 out.z = v1.x*v2.y - v1.y*v2.x;

 // Normalize
 out.Norm();

 // Done
 return out;
}

Efekt jest widoczny po prawej (wektor normalny został zaprezentowany jako XYZ->RGB, jest to standardowy zabieg). Po powiększeniu obrazka widać niezły szum wynikający z niedokładności obranej metody (głównie chodzi o to ze normale powinny w tym przypadku być liczone z większej ilości punktów, a nie tylko z trzech). Aby go usunąć wystarczy zwykły blur 3x3->1x1. Blur wykonywany jest w tej samej funkcji (cały czas MakePicture()), za pomocą następującego kodu (wykonywanego dla każdego punktu heightmapy):

 // This is a simple blur and nothing more
 NormalMap[x + z * HMAP_WIDTH] = (
   PreNormalMap[x - 1 + z * HMAP_WIDTH] +
   PreNormalMap[x     + z * HMAP_WIDTH] +
   PreNormalMap[x + 1 + z * HMAP_WIDTH] +
   PreNormalMap[x - 1 + (z + 1) * HMAP_WIDTH] +
   PreNormalMap[x     + (z + 1) * HMAP_WIDTH] +
   PreNormalMap[x + 1 + (z + 1) * HMAP_WIDTH] +
   PreNormalMap[x - 1 + (z - 1) * HMAP_WIDTH] +
   PreNormalMap[x     + (z - 1) * HMAP_WIDTH] +
   PreNormalMap[x + 1 + (z - 1) * HMAP_WIDTH]) * (1.0f / 9.0f);

Normalmapa po blurze wygląda lepiej (patrz lewa strona). Dodam że z uwagi iż normale się troochę liczą, zrobiłem cache'owanie ich do pliku normal.cache (zajmuje jakieś 200mb).

A teraz powrót do słupków. Ponieważ rysowaniu słupka trwa dłużej niż rysowanie pixela (ktoś zaskoczony ?;p) nie można opierać się na rysowaniu słupków real-time. Można natomiast zrobić małe obliczenia wstępne, co do tego który pixel na ekranie zostanie wypełniony przez który słupek - dzięki temu otrzyma się tablicę translacji ekran-%gt;heightmapa. Jest to ostatnia rzecz robiona w funkcji MakePicture, a jej implementacja (dla każdego punktu heightmapy) wygląda następująco:

 // Get the heightmap data
 float max_y = hmap[x + z * HMAP_WIDTH];

 // Bar top and bottom
 int y_from = (HEIGHT - 1) - (int)base_y + 100;
 int y_to   = (HEIGHT - 1) - (int)base_y - (int)max_y + 100;

 // Does reach out of the screen ? Fir it then
 if(y_from < 0)          y_from = 0;
 if(y_to   < 0)          y_to   = 0;
 if(y_from > HEIGHT - 1) y_from = HEIGHT - 1;
 if(y_to   > HEIGHT - 1) y_to   = HEIGHT - 1;

 // Lift the minimal y ?
 if(y_to < total_min_y)
   total_min_y = y_to; // Yep

 // "Draw" the bar
 for(y = y_from; y > y_to; y--)
 {
   RenderCache[x + y * WIDTH] = x + z * HMAP_WIDTH;
 }

Wyliczanie minimalnego y wynika z kolejnej optymalizacji, opierającej się na oczywisty fakcie mówiącym "nie warto rysować czegoś czego nie ma".

Teraz krótka przerwa na omówienie dalszej architektury programu. Opisany wyżej MakePicture() jest wykonywany raz na samym początku programu, jeszcze przed utworzeniem okna. Dalsza część programu jest natomiast interaktywna, i wykonywana N razy na sekundę. Z uwagi na przyjęty model renderingu (wyliczanie koloru pixeli na podstawie wysokości heightmapy oraz świateł, czyli w sumie standardowy pixel shader) cała reszta może zostać wykonana wielu wątkach. W moim przypadku użyte są 4 wątki (akurat posiadam Quad'a w desktopie), przy czym każdy wątek renderuje 1/4 ekranu (poziome bloki ekranu). Oprócz 4rech renderujących wątków, jest jeszcze jeden koordynujący je (on głównie śpi, a jak już się budzi to tylko po to by zrobić SDL_Flip()), oraz jeszcze jeden który zajmuje się zdarzeniami (ruch myszki, naciśnięcie ESC, etc). Jeśli chodzi o co-gdzie, to Render() to finalny "pixel shader" (software'owy ofc), RenderWorker() to prawie że wrapper na Render(), zajmujący się dodatkowo komunikacją między wątkową (to duże słowo, szczególnie że zrobiłem to trochę na skróty). Dalej, RenderProc() rysuje tło (niebo - tylko raz), a następnie synchronizuje wątki, śpi, i wywołuje SDL_Flip(), oraz main() na którego końcu jest pętla zajmująca się eventami.

Jeszcze pół słowa o niebie - jest to najzwyklejszy w świecie gradient, nie ma tutaj żadnego dynamicznego obliczania koloru nieba. Kod rysujący gradient to:

 // Generate background
 //  float bg_start[3] = { 32.0f, 69.0f, 113.0f };
 float bg_start[3] = { 96.0f, 128.0f, 190.0f };
 //float bg_end[3]   = { 168.0f, 228.0f, 236.0f };
 float bg_end[3]   = { 255.0f, 255.0f, 255.0f };
 float bg_diff[3]  = { (bg_end[0] - bg_start[0]) / (float)(HEIGHT*18/40),
                       (bg_end[1] - bg_start[1]) / (float)(HEIGHT*18/40),
                       (bg_end[2] - bg_start[2]) / (float)(HEIGHT*18/40) };

 // Render the background (it has to be done only once)
 for(y = 0; y < HEIGHT; y++, bg_start[0] += bg_diff[0], bg_start[1] += bg_diff[1], bg_start[2] += bg_diff[2] )
 {
   for(x = 0; x < WIDTH; x++)
   {
     img[x + y * WIDTH].b = (unsigned char)bg_start[0];
     img[x + y * WIDTH].g = (unsigned char)bg_start[1];
     img[x + y * WIDTH].r = (unsigned char)bg_start[2];
   }
 }

Kod jest prosty, więc pominę jego opis.

Czas na "pixel shader". Na finalny efekt składają się 3 rzeczy:
1) "mgła" wynikająca z odległości obserwatora od punktu oraz coś co można uznać za ambient light (światło otoczenia)
2) światło rozproszone (diffusive)
3) światło refleksyjne (specular)
Przy czym oba światła mam trochę oszukane jeśli chodzi o wzór (zmieniałem je podczas eksperymentów, tak żeby mi jak najbardziej efekt końcowy pasował). Najpierw liczony jest kolor tła (interpolacja dwóch kolorów), następnie obliczany jest dot product wektora normalnego pixela (ścianki) oraz wektora światła padającego na tenże pixel, a później liczone są światła. Dot product wychodzi następujący (przypadki gdy światło jest po lewej na górze i po prawej na dole ekranu):



Finalny kod odpowiedzialny za liczenie ostatecznego koloru dla każdego pixela wygląda następująco (po prawej są obrazki, kolejno mgła+ambient, diffusive zaznaczone na czerwono, i specular zaznaczone na czerwono na kolejnym obrazku):

 static float fg_start[3] = { 23.0f, 38.0f, 61.0f };
 static float fg_end[3]   = { 200.0f, 237.0f, 243.0f };
 static float fg_diff[3]  = { (fg_end[0] - fg_start[0]) / (float)(HMAP_DEPTH),
                       (fg_end[1] - fg_start[1]) / (float)(HMAP_DEPTH),
                       (fg_end[2] - fg_start[2]) / (float)(HMAP_DEPTH) };

 [...]

 // Get the height
 float max_y = hmap[idx];
 z = idx / HMAP_WIDTH;

 // Calc color
 Vector3D color = Vector3D(
   (fg_start[0] + fg_diff[0] * (float)z) / 255.0,
   (fg_start[1] + fg_diff[1] * (float)z) / 255.0,
   (fg_start[2] + fg_diff[2] * (float)z) / 255.0
   );

 Vector3D vp_color = color;

 // Sun light

 // Setup vectors
 Vector3D vp = Vector3D( (float)x, (float)max_y, (float)z );

 Vector3D L = sun_pos - vp;

 L.Norm();
 Vector3D N = NormalMap[idx];


 float per = 0;
 per = ((float)(z/* - 2*HMAP_WIDTH/4*/) / (float)HMAP_DEPTH);
 per *= per;
 per *= per;
 per *= per;
 per = 1.0f - per;

 // Diffusive
 float dot;
 dot = L.Dot(NormalMap[idx]);
 if (dot < 0.0)
 {
   float diff = -dot * 0.1f * per; // Play with this to get nice effects
   color += (sun_color * vp_color) * diff;
 }

 // Diffusive 2
 if (dot < -0.2)
 {
   float diff = dot*dot*dot*dot*dot*dot * 0.5f * per; // Play with this to get nice effects
   color += sun_color * diff;
 }

 // Specular
 Vector3D R = L -  N * L.Dot(N) * 2.0l;
 Vector3D Cs = Vector3D(0, max_y, max_y);
 Cs.Norm();
 dot = Cs.Dot(R);
 if (dot < 0.0)
 {
   dot = pow(dot, 40.0);
   float spec = dot * (0.2f * per); // Play with this to get nice effects
   color += sun_color2 * spec;
 }

 // Check
 if(color.arr[0] > 1.0f) color.arr[0] = 1.0f;
 if(color.arr[1] > 1.0f) color.arr[1] = 1.0f;
 if(color.arr[2] > 1.0f) color.arr[2] = 1.0f;

 // Write pixel color
 // Uncomment other shaders to see the normals or the dot product

 // Shader - full
 img[x + y * WIDTH].b = (unsigned char)(color.arr[0] * 255.0f);
 img[x + y * WIDTH].g = (unsigned char)(color.arr[1] * 255.0f);
 img[x + y * WIDTH].r = (unsigned char)(color.arr[2] * 255.0f);


Zmieniając kolor nieba i terenu można oczywiście uzyskać ciekawe efekty:



Można też dodać trochę GIMPa ;D



OK, chyba tyle. Na koniec linki do kodu i do filmiku:

Sky.zip (6mb) - źródło SDL (SDL wymagany, 1.2.12), Linux/Windows/MacOSX, z height mapą
Sky_SDL.zip (6mb) - źródło SDL (SDL wymagany, 1.2.12) + binarka Windows, z height mapą
Sky_Gdi.zip (10kb) - źródło WinAPI (GDI), Windows only, bez height mapy
sky.avi (1mb) - filmik

Kompilacja:
Windows Vista SP1 (g++ Sky.cpp Vector3D.cpp -lSDL)
MacOSX 10.5.5     (g++ `sdl-config --cflags` Sky.cpp Vector3D.cpp `sdl-config --libs`)
Ubuntu 8.10       (g++ `sdl-config --cflags` Sky.cpp Vector3D.cpp `sdl-config --libs`)