Post jest przeznaczony dla początkujących programistów (część o kodowaniu może zainteresować również bardziej doświadczone osoby). Planowałem go napisać już jakiś czas temu, przy okazji kolejnego pytania kolejnej osoby, które brało się z niepełnego zrozumienia czym jest zmienna/stała, a konkretniej np. nierozróżnienia wartości zmiennej od reprezentacji wartości, a także od kodowania i zapisu zmiennej w pamięci. Niniejszy post ma na celu wyjaśnienie wspomnianych różnic.

Wersja PDF (405KB, 18 stron): zmienne.pdf
(dla zainteresowanych re-publikacją: notka odnośnie zasad kopiowania znajduje się na dole postu/PDFa)

Zanim zacznę

Dla ułatwienia będę podawał przykłady dotyczące architektury x86 w trybie 32-bitowym (chociaż sporo z nich można przenieść też na inne architektury), a więc założę m.in. że bajt ma 8 bitów, że pamięć jest adresowana względem bajtów (a nie np. bitów czy wordów), oraz wspomnę kodowania i zapis używane na tej platformie.
Będę również pisał "zmienna" mając na myśli zarówno zmienne jak i stałe - z punktu widzenia CPU dużej różnicy nie ma - to i to są po prostu pewnymi danymi które się przetwarza. Fakt, że stałe zazwyczaj są dostępne bezpośrednio ze strumienia instrukcji (patrz immediate w assembly) lub rezydują w pamięci tylko do odczytu, jest w tym wypadku bez znaczenia.
Część o kodowaniu polecam przede wszystkim programistom zainteresowanym językami niskopoziomowymi (C/C++/Assembly), niemniej jednak programiści piszący w językach wyższego poziomu (Java, C#, PHP) również mogą znaleźć tam trochę interesujących informacji - w końcu engine Java'y, PHP, etc jest napisany w C/C++, więc nawet jeśli nie można operować bezpośrednio na zakodowanej postaci zmiennej, to jednak ona gdzieś tam głębiej siedzi, a więc problemy typu integer overflow czy brak odwzorowania we floatach, dotyczą również tych języków.

W skrócie

Punktem wyjścia jest fakt, że zmienna ma pewną wartość, oraz że ta wartość jest de facto jednym z elementów zbioru możliwych wartości dla danego typu zmiennej, który to typ jest ściście związany z użytym kodowaniem zmiennej.
Wartość zmiennej w postaci zakodowanej może być dodatkowo np. zapisana w pamięci RAM.
Wartość zmiennej można reprezentować na wiele różnych sposobów, np. namalować wartość na ekranie jako liczbę dziesiętną lub szesnastkową, lub wypisać wszystkie możliwe wartości i zaznaczyć odpowiednią wartość np. wskazówką (patrz zegar analogowy).

Tak więc wyodrębniłbym tutaj 4 warstwy:

bliżej człowieka	Reprezentacja (i sposób reprezentacji)	np. liczba w systemie dziesiętnym , liczba w systemie hexadecymalnym, liczba w zapisie rzymskim np. 42, 0x2A, XLII
↑	Wartość	np. 42
↓	Zakodowana wartość (i kodowanie / typ)	np. 32-bit U2 (aka Two's complement) np. 0x0000002A
bliżej CPU	Zapisana wartosć (i zapis)	np. Little Endian np. 2A 00 00 00

Reprezentacja

Reprezentacja zmiennej to wyświetlenie (zaprezentowanie) jej wartości w jakiś z góry ustalony sposób. Zacznę od najpopularniejszej obecnie formy reprezentacji wartości całkowitej 1234:

1234
Liczba w systemie dziesiętnym. De facto, taka liczba to kilka znaków graficznych, zwanych cyframi ("liczba" a "cyfra" to dość istotne rozróżnienie), zapisana wg odpowiednich zasad: cyfry 0-9, ostatnia cyfra po prawej reprezentuje jednostki (10**0, pisząc ** mam na myśli "do potęgi"), kolejna (idąc w lewo) dziesiątki (10**1), etc. Oczywiście, żeby wymalować te cyfry na ekranie, musiałem najpierw je sprowadzić do postaci indeksów/selektorów (aka kodów ASCII / Unicode / etc) odpowiednich malunków graficznych w zestawie takich malunków (znaków w czcionce) - patrz rysunek niżej.



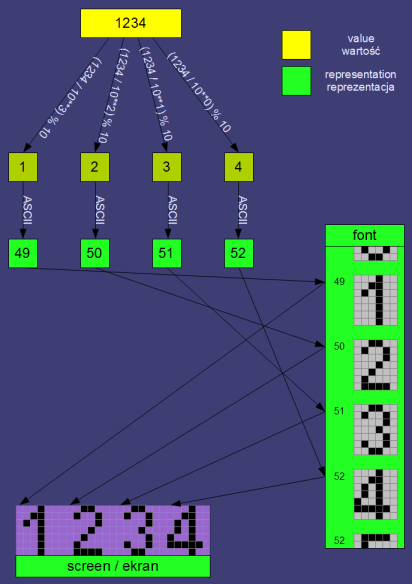
I tutaj krótka uwaga - reprezentacja wartości jest dla CPU zupełnie nieczytelna. Dla CPU powyższa "liczba" będzie:
- monochromatyczną lub kolorową bitmapą, czyli de facto dwu-wymiarową tablicą pixeli, a raczej kolejnych wartości kolorów RGB dla każdego pixela
- lub, w najlepszym razie (jeśli nadal ta "liczba" leży gdzieś w pamięci) ciągiem czterech znaków ASCII o kodach 49, 50, 51 i 52 (to oczywiście kody ASCII/Unicode znaków '1', '2', '3' oraz '4').

Aby CPU ponownie "zrozumiał" tą liczbę, należy przeprowadzić konwersję reprezentacji do wartości (czyli konwersję w drugą stronę).
W przypadku gdy mamy liczbę jako tekst (czyli ciąg kodów np. ASCII), to w języku C/C++ możemy skorzystać z funkcji np. atoi lub scanf z parametrem %i. W przypadku gdy mamy tylko bitmapę (rzadki przypadek), najpierw trzeba użyć OCRa (co kapkę utrudnia sprawę, ale nadal jest możliwe do wykonania).
Analogicznie w drugą stronę - jeśli chcemy zaprezentować jakąś wartość, musimy dokonać odpowiedniej konwersji, np. konwersję wartości całkowitej na w/w ciąg kodów ASCII.

Dygresja: Zazwyczaj do tych konwersji używa się dostępnych funkcji które to robią za nas, natomiast dobry programista powinien umieć, w razie potrzeby, sam zaimplementować odpowiednie konwertery. Dodam, że jest to jedno z ćwiczeń z którym prawie na pewno spotkają się studenci pierwszego roku na kierunkach informatycznych.

Na koniec tej części jeszcze kilka innych spotykanych form reprezentacji wartości (nadal dla przykładowej wartości całkowitej 1234):

0x4D2
Czyli zapis hexadecymalny (lub po prostu "hexa" / "w hexach"), czyli w systemie szesnastkowym (k=16). Dodam że "0x" tutaj jest pewnym ozdobnikiem, który mówi czytającemu, że to jest liczba w hexach; można również spotkać się z innymi ozdobnikami przy hexach, jak np.:
$4D2 (Turbo Pascal / Delphi)
4D2h (różne assemblery; jeśli liczba zaczyna się od cyfry A-F, to poprzedza się ją dodatkowym zerem, np. 0ABCDh)
&4D2 (Locomotive Basic np. na Amstradach)
4D2 (bez dekoratora, zalecane tylko w przypadku gdy z kontekstu wynika że liczba będzie w hexa)
Po więcej przykładów dekoratorów odsyłam na wiki.

Dygresja: Spotkałem się z przekonaniem, że dowolna liczba zaprezentowana w postaci hexadecymalnej jest pointerem/adresem. Oczywiście to przekonanie jest nieprawdziwe, ponieważ nawet jeśli na logicznym poziomie dana wartość nie jest pointerem/adresem, to i tak można ją wypisać hexadecymalnie.

Oczywiście liczbę można reprezentować w bardzo różnych systemach liczbowych. Z innych popularnych jest jeszcze binarny (dwójkowy, k=2) oraz ósemkowy (k=8). Studenci pewnie spotkają się jeszcze z minus-dwójkowym (k=-2) i resztą naturalnych podstaw (k=3 do 36). Należy pamiętać o tym, że podstawa systemu (czyli "k") nie musi być ani liczbą całkowitą (np. k=3.1337), ani też stała dla różnych pozycji (np. k={4,2,6,8,2,5,3,7,9,...} dla kolejnych pozycji).

tysiąc dwieście trzydzieści cztery
Zapis słowny w języku polskim. Obecnie stosowany głównie w ramach ćwiczeń dla studentów programowania, przy wypełnianiu blankiecików na poczcie / faktur oraz przy dyktandach na polskim. Natomiast niewątpliwie jest to forma reprezentacji wartości.

.---- ..--- ...-- ....-
Tak... to kod Morse'a.

MCCXXXIV
A to ofc zapis rzymski (konwerter wartości do reprezentacji rzymskiej jest kolejnym popularnym ćwiczeniem na studiach).


Wartość oczywiście można zaprezentować równiez "bardziej" graficznie - np. w postaci progress bara. Oczywiście w takim przypadku dodatkowym parametrem jest "maksymalna wartość" progress baru - w tym wypadku jest to 10000.
Dodatkowo w tym wypadku wartość pokazana jest niejako redundantnie: graficznie (pasek postępu) + w postaci liczby dziesiętnej (namalowanej na tym pasku).

W przypadku gdy mamy zestaw wartości, to popularną metodą ich reprezentacji jest wykres (konwersja "w drugą stronę" - wykresu do wartości jest ciekawym ćwiczeniem, patrz Zadanie 4 z Security Days 6).

W ramach ćwiczenia zachęcam to wymyślenia jeszcze innych możliwych lub używanych reprezentacji liczby całkowitej :)

Wartość

Wartość zmiennej można wytłumaczyć na kilka sposobów.
Z jednej strony jest to jeden wybrany element ze zbioru elementów możliwych wartości.
Z drugiej strony jest to pewna wielkość, na której wykonuje się pewne operacje, i która może być w jakiś sposób zinterpretowana.
Z trzeciej strony, wartość jest interpretacją sekwencji bitów wg. danego kodowania.

Dla nas najistotniejszy jest fakt, że wartość jest to jakaś wielkość (lub zestaw/zbiór wartości) na której są wykonywane operacje matematyczne (np. dodawanie, odejmowanie, mnożenie, potęgowanie, etc) lub inne (np. zmiana dużych liter na małe), a konkretniej - dany język, CPU, czy też biblioteka, jest przystosowana do wykonywania operacji np. matematycznych na danej wartości.
Można wartość traktować jako "natywną reprezentację wielkości" na danej platformie/architekturze/etc.

Dygresja: Bardzo rzadko zdarza się by operacje wykonywało się bezpośrednio (bez żadnych libów/funkcji) na nie-natywnej reprezentacji - jest to po prostu niewygodne (ale możliwe).
De facto implementacja kodowania sprowadza się do stworzenia zestawu funkcji które umożliwią operowanie na wartościach w innej niż natywna reprezentacji.

Wspomniałem wcześniej o zbiorze możliwych wartości dla danej zmiennej, który wynika bezpośrednio z kodowania. Zapewne większość z Was spotkała się wcześniej z tzw zasięgiem zmiennej, czyli np. z jakąś tabelką w której było napisane, że "char" przyjmuje wartości całkowite "od -128 do 127", a "unsigned short" przyjmuje wartości naturalne (+0) "od 0 do 65535" - to są właśnie zbiory możliwych wartości (dlaczego są takie a nie inne, wyjaśnię następnej sekcji).

Sprawa się kapkę komplikuje np. w przypadku floatów lub double float (tzw. liczb zmiennoprzecinkowych) - o ile łatwo powiedzieć jaka jest maksymalna i minialna wielkość którą można zapisać (wybrać) w zmiennej typu float, to raczej (prawie?) nikt nie umiałby łatwo wymienić kolejnych (np. rosnąco) możliwych wartości, co w przypadku np. int'a jest przecież trywialne.
Przykładowo, następną możliwą wartością po 10 jest 10.000000953674316, więc można by się spodziewać, że następną możliwą wartością po 1000 będzie analogicznie 1000.000000953674316 - w rzeczywistości tak nie jest, i następną możliwą wartością jest 1000.0000610351562 (czyli wartość o ponad dwa dziesiętne rzędy wielkości większa).
Dlaczego tak się dzieje? No cóż, wynika to z kodowania :)

By the way...
On 22nd Nov'24 we're running a webinar called "CVEs of SSH" – it's free, but requires sign up: https://hexarcana.ch/workshops/cves-of-ssh (Dan from HexArcana is the speaker).

Oczywiście, zbiór wartości dla niektórych typów, w szczególności typu wyliczeniowego, można zdefiniować samemu:

enum moje_ulubione_kolory {
 BRUNATNY, LILAROZ, KREMOWY, KAWAZMLEKIEM, MORSKINIEBIESKI
} kolor = BRUNATNY;
Czasami (na pewnym poziomie abstrakcji) jedna zmienna może przyjmować kilka wartości na raz - tak dzieje się w przypadku tzw "flag" (na poziomie assembly obsługa flag jest całkiem niezła, chociaż i tak się z niej nie korzysta):

#define FLAG_ALIGN_LEFT 1
#define FLAG_ALIGN_TOP  2
#define FLAG_BORDER     4
#define FLAG_BIG_PADDING 8
unsigned int Design = FLAG_ALIGN_LEFT | FLAG_BORDER;
Oczywiście, wartość tej zmiennej można zinterpretować zarówno jako "5" (1+4) jak i jako zestaw dwóch wartości: "FLAG_ALIGN_LEFT" oraz "FLAG_BORDER".

Wartość na poziomie logicznym
Mimo że operujemy na wartości jako na liczbie (lub ciągu znaków), to z bardziej abstrakcyjnego punktu widzenia, ta dana zmienna/wartość coś opisuje i można ją zinterpretować.
Przykładowo, wartość 34 może być dla nas wiekiem użytkownika (np. w latach), lub prędkością z jaką porusza się postać na planszy (np. w pixelach na sekundę).
Tak więc jedną z podstawowych umiejętności w programowaniu (zresztą dość łatwą do nabycia) jest umiejętność stwierdzenia jakich zmiennych potrzebujemy do rozwiązania danego problemu, co one będą opisywać i jak będziemy interpretować ich wartość, a także umiejętność dobrania odpowiedniego typu (kodowania).

Kodowanie i typ zmiennej

Typ zmiennej mówi o:
- rodzaju wartości które można w zmiennej tego typu zapisać (np. liczby całkowite)
- czasem o wielkości zmiennej (czyli ile bitów można na zmienną poświęcić, np. 8, 16, 32, 40, 80, etc)
Typ jest też powiązany z użytym kodowaniem, a co za tym idzie, także zestawem możliwych wartości.

Kodowanie (w tym przypadku), to pewien zestaw zasad mówiących o tym jak zapisać daną wartość mając do dyspozycji nośnik w postaci serii bitów (ciekawostka: bit to skrót od "BInary digiT", czyli "cyfra dwójkowa") - w końcu CPU operuje na bitach (patrz bramki logiczne, sumatory, etc).
Zacznijmy od tego, że mamy do wyboru kilka zapisów liczby naturalnej w postaci binarnej, np.:
- kod 1 z n
- naturalny system binarny (k=2)
- kod Gray'a i pochodne
- kod Johnsona
- kod BCD (Binary Coded Decimal)
Do zapisu liczb całkowitych służą inne kodowania, np.:
- któreś z powyższych, poświęcając najstarszy bit na bit znaku
- kod uzupełnieniowy do jedności (analogicznie jak powyżej, tylko że liczba ujemna jest zapisywana z dodatkową negacją bitów)
- kod uzupełnieniowy do dwóch (ZU2 albo U2, eng. Two's complement)
- system minusdwójkowy (k=-2)
W przypadku liczb niecałkowitych, tj. wymiernych lub rzeczywistych, używa się np.:
- kodowania stałopozycyjnego (tzw. fixed point)
- kodowania zmiennoprzecinkowego - np. IEEE 754 binary32 lub IEEE 754-2008 decimal128

Oczywiście, do tego dochodzi kodowanie tekstu (np. UTF-8, ASCII, etc), które jest same w sobie tematem na osobny post. Dla osób zainteresowanych hackingiem/security dobra znajomość kodowań typu UTF-8 czy UTF-7 jest obowiązkowa.

Dla przykładu opisze kilka typów zmiennych z języka C (x86, 32-bit) i używanych przez nich kodowań.

Jeszcze krótka uwaga: zapis zakodowany danej wartości będę reprezentował w hexa; podawanie wartości poszczególnych bitów (w postaci serii zer i jedynek) na dłuższą metę jest nieczytelne i niewygodne. Wystarczy pamiętać, że każdy nibble (tak nazywa się "cyfra hexa") to po prostu zestaw czterech bitów zaprezentowany jako jedna cyfra hexadecymalna (1-9 A-F), np. bity 1010 zostaną zaprezentowane jako A.

unsigned char
Wielkość: 8 bitów
Kodowanie: naturalne binarne
Możliwe wartości: liczby naturalne (+0), od 0 do 255 (czyli razem 256 różnych wartości)
Kody od 01 do FF to liczby dodatnie (kolejno 01 to 1, 02 to 2, 03 to 3, etc).
Kod 00 to oczywiście 0.

Co się stanie jeśli do wartości 255 (ostatnia liczba naturalna jaką można w unsigned char zapisać) dodamy 1? A co się stanie jeśli od wartości 0 odejmiemy 1?
Zachęcam do sprawdzenia samodzielnie :)

Zjawisko które w tych przypadkach występuje nosi nazwę integer overflow (w pierwszym przypadku) oraz integer underflow (w drugim przypadku), i jest specyficzne dla wszystkich intów, zarówno signed jak i unsigned, na x86 (oczywiście wartości graniczne są zależne od kodowania i wielkości). Zachęcam do rzucenia również okiem na ten post.
Dodam że w niektórych przypadkach integer over/underflow prowadzi bezpośrednio do sporych problemów z bezpieczeństwem aplikacji.

signed int
Wielkość: 32 bity
Kodowanie: U2
Możliwe wartości: liczby całkowite od -2147483648 do 2147483647 (czyli razem 4294967296 różnych wartości)
Kody od 00000001 do 7FFFFFFF to liczby dodatnie (analogicznie jak w przypadku char).
Kody od FFFFFFFF do 80000000 to liczby ujemne (FFFFFFFF to -1, FFFFFFFE to -2, etc).
Kod 00000000 to oczywiście 0.
Ciekawą rzeczą która wynika z użycia kodowania U2 w przypadku signed int, jest to, że liczb ujemnych jest o jeden więcej niż liczb dodatnich. Powoduje to pewne komplikacje w dwóch przypadkach:

1. Wartość bezwzględna z liczby -2147483648 jest równa -2147483648 (sic!) - zachęcam do sprawdzenia:
int x = 0x80000000;
printf("x=%i, -x=%i, abs(x)=%i\n", x, -x, abs(x));

$ gcc -Wall -Wextra test.c
$ a
x=-2147483648, -x=-2147483648, abs(x)=-2147483648
Powyższe zachowanie wynika bezpośrednio z zapisu liczb ujemnych w U2, a konkretniej tego jak na poziomie bitowym wygląda operacja zmiany znaku:
x_new = -x_old → x_new = (~x_old) + 1; (~ to oczywiście negacja bitowa / dopełnienie bitowe)
(ponownie, zachęcam do przetestowania)
Czyli w przypadku -2147483648 która w postaci zakodowanej to 0x80000000 cały proces zmieny znaku będzie wyglądał następująco
(~0x80000000) + 1 → 0x7FFFFFFF + 1 → 0x80000000

Należy zaznaczyć, że w man'ie abs() jest informacja, że abs z minimalnego int'a jest UB (undefined behavior).

2. Próba podzielenia wartości -2147483648 przez -1 (co powinno dać 2147483648, ale ta liczba nie znajduje się w zestawie możliwych wartości w 32-bitowym U2) skończy się "wykrzaczeniem" programu (exception #DE (division error) jest rzucany przez CPU).



Zachęcam do sprawdzenia samemu:
#include <stdio.h>

int my_div(int a, int b) {  return a / b; }

int main(void)
{
 int x = 0x80000000;
 printf("wynik = %i\n", my_div(x, -1));

 return 0;
}

// Program received signal SIGFPE, Arithmetic exception.
// 0x004013c7 in my_div (a=-2147483648, b=-1) at test.c:6
// 6         return a / b;
Tak więc pisząc "kalkulatory", pamiętajcie, że nie wystarczy sprawdzić czy dzielnik nie jest równy zero :)

Dygresja: Na poziomie assembly jest dużo więcej wartości które mogą "wykrzaczyć" dzielenie via IDIV i DIV, ponieważ w tych instrukcjach dzielna jest zawsze dwa razy większa niż dzielnik (np. 64 bity dzielnej i 32 bity dzielnika), a wynik zapisywany jest w rejestrze wielkości dzielnika (np. 32 bitowym) - łatwo więc wyobrazić sobie sytuację w której w wyniku otrzyma się liczbę niedającą się zapisać w 32 bitach.

Oczywiście, zjawisko integer overflow i underflow również w tym wypadku występują.

By the way...
On 22nd Nov'24 we're running a webinar called "CVEs of SSH" – it's free, but requires sign up: https://hexarcana.ch/workshops/cves-of-ssh (Dan from HexArcana is the speaker).

Ćwiczenie: napisz dwie funkcje, pierwsza która dodaje dwa inty, druga która mnoży dwa inty; funkcje mają zwracać dodatkową wartość, mówiącą o tym czy nastąpił integer overflow lub integer underflow.

float
Wielkość: 32 bity
Kodowanie: IEEE 754 (single precision 32-bit)
Mapa:
bity 0-22 (włącznie) - mantysa
bity 23-30 (włącznie) - wykładnik
bit 31 - znak
Możliwe wartości: wartości w przedziale +-3.4028235e38
No i tutaj zaczyna się prawdziwa zabawa. Mianowicie, float jest typem zmiennoprzecinkowym - oznacza to mniej więcej tyle (w pewnym uproszczeniu), że mamy stałą liczbę bitów na której możemy zapisać liczbę (mantysa), a następnie możemy wybrać w którym postawić przecinek (wykładnik), np. (uproszczenie):

  123456,0
  12345,6
  1234,56
  123,456
  12,3456
  1,23456
  0,123456
  0,0123456

etc.
Jedną z konsekwencji tego, jest fakt, że między np. 10 a 11 jest duużo więcej możliwych wartości, niż między 10000 a 10001. Również, jak wspomniałem wcześniej, kolejna możliwa wartość po danej liczbie jest strikte zależna od tej liczby (tj. ile bitów już zostało "zużyte" na zapisanie liczby "przed przecinkiem").
Przykładowa tabela prezentująca ilość wartości między dwoma liczbami oraz najbliższą kolejną wartość po danej liczbie, znajduje się poniżej:

         

Od	Do (Od+1)	Ilość możliwych wartości między [Od, Do)	Kolejna możliwa wartość po Od
0.0	1.0	1065353217	0.000000000000000 00000000000000000 00000000000014013
1.0	2.0	8388608	1.0000001192092896
2.0	3.0	4194304	2.0000002384185791
10.0	11.0	1048576	10.000000953674316
100.0	101.0	131072	100.00000762939453
1000.0	1001.0	16384	1000.0000610351562
10000.0	10001.0	1024	10000.0009765625
100000.0	100001.0	128	100000.0078125
1000000.0	1000001.0	16	1000000.0625
10000000.0	10000001.0	1	10000001.0*
100000000.0	100000001.0	0	100000008.0*

* W miarę zbliżania się do stosunkowo dużych liczb, dochodzi do sytuacji w której nie można już zapisać nic "po przecinku", lub nawet nie można zapisać kolejnych liczb całkowitych. Daje to dość zabawne efekty - np. 100000000 + 3 = 100000000, a 100000000 + 6 daje 100000008 (sic!). Tak więc, poniższy kod jest nieskończoną pętlą (mimo że na to nie wygląda):
 float f;
 for(f = 100000000.0f; f < 100000008.0f; f+=1.0f)
   printf("%f\n", f);
 Dygresja: Powyższa tabelka ma pewną wadę - mianowicie przykłady są (w większości) iloczynem liczby 10 (jakoś tak wyszło, że jesteśmy przyzwyczajeni do tego systemu), natomiast float używa systemu dwójkowego jako podstawy, więc trochę więcej by powiedziała tabelka z kolejnymi potęgami dwójki jako "Od". Dodam, że nowy standard IEEE-754-2008 przewiduje również liczby zmiennoprzecinkowe o podstawie k=10, co przyda się do pewnych zastosowań. Niektóre kompilatory, np. GCC, wprowadziły już nawet odpowiednie typy zmiennych (np. _Decimal32). Nie zanosi się jednak na to, zeby na x86 to kodowanie doczekało się natywnej implementacji na poziomie CPU (więc póki co operacje na tych typach są "emulowane").

W tym miejscu warto podać wzór na wyliczenia wartości z zakodowanego floata:

wartość = (-1)**znak * 1.mantysa * 2**(wykładnik - 127)

(dodam że mantysa i wykładnik są kodowane w naturalnym systemie binarnym)
Zainteresowanych zachęcam do rzucenia okiem na wiki lub do samego standardu IEEE 754, ponieważ sprawa jest w rzeczywistości jeszcze trochę bardziej skomplikowana - powyższy wzór służy do dekodowania wartości, ale tylko w przypadku tzw. wartości znormalizowanych (taka specyficzna cecha IEEE 754). W przypadku liczb zdenormalizowanych wzór używa "-126" przy obliczeniu potęgi dwójki, oraz 0.mantysa zamiast 1.mantysa.

Należy jeszcze dodać, że float ma kilka specjalnych wartości:
NaN (Not a Number) - np. pierwiastkowanie kwadratowe liczby ujemnej da w wyniku NaN (dodam, że NaN można zakodować na 2**24-2 różnych sposobów); dowolna operacja przeprowadzona na NaN zwraca NaN, a dowolny test (np. ==, < albo >) zwraca false.
+Inf, -Inf (Infinity) - czyli nieskończoność, może powstać w wyniku np. dzielenia przez zero (dowolne operacje na +-Inf dają w wyniku +-Inf, oprócz oczywiście np. pierwiastka kwadratowego z -Inf, które daje NaN, oraz operacji zmiany znaku, która daje przeciwny -+Inf);
+0, -0 (zero) - z uwagi na wydzielenie dodatkowego bitu na znak, doszło do sytuacji w której są dwa zera - zero dodatnie oraz zero ujemne (w obliczeniach przyjmuje się, że zera są sobie ofc równe, czyli +0.0f == -0.0f zwróci true).

OK, to teraz pytanie - skoro wiemy jak wartość jest zakodowana, to... jak się w zasadzie dobrać (w C/C++) do tej zakodowanej postaci? Lub w drugą stronę - mając zakodowaną postać, jak ją zdekodować (sprowadzić do wartości natywnej)? Zanim do tego przejdę najpierw chciałbym omówić jeszcze...

Zapis w pamięci

Czyli Little-Endian (dalej LE) vs Big-Endian (dalej BE), a także słowo o Middle/Mixed-Endian (dalej ME).

Mamy więc np. 32-bitową zmienną, która jest nawet już zakodowana np. w U2. No i teraz pojawia się pytanie - jak to zapisać w pamięci adresowanej per bajt (czyli 8-bitów).
Zauważcie, że są przynajmniej dwie (a w zasadzie trzy) możliwości:

Możliwość 1:
Zmienna 32-bitowa ma bity ponumerowane od 0 do 31. Weźmy więc pierwsze 8 bitów (0-7) i zapiszmy w pierwszym bajcie, 8 kolejnych w drugim, etc. Ten sposób nazywa się Little Endian i korzysta z niego np. x86.

Np. zmienna 32-bitowa U2 która ma postać zakodowaną 0x12345678, będzie w pamięci zapisana następująco (krótka uwaga: fakt, że pamięć jest adresowana per bajt należy uwzględnić przy reprezentacji zapisu w pamięci - zazwyczaj stosuje się hexadecymalny zapis (2 cyfry hexa tworzą jeden bajt) oddzielając bajty spacjami):

0x12345678 → 78 56 34 12

Czyli postać zakodowana została zapisana "bajtami od tyłu".
Ważne: początkujący często zapisują po prostu liczbę od tyłu (np. 87 65 43 21) - ale jest to oczywiście błąd, ponieważ jeden bajt jest tworzony przez dwa nibble, a kolejność wewnątrz bajtu się nie zmienia, zmienia się tylko kolejność bajtów..

Możliwość 2:
Ponieważ powyższy zapis w pamięci wygląda trochę nienaturalnie, to stwierdzono, że w zasadzie dużej różnicy nie zrobi jeśli zapisze się tą liczbę bardziej "naturalnie dla człowieka", czyli od najbardziej znaczących bajtów do najmniej znaczących - mowa ofc o Big Endian (zwanym również Network Safe Endian, albo Network Endian z uwagi na częste stosowanie w "binarnych" protokołach sieciowych). Przykładowa liczba będzie wyglądała następująco (należy pamiętać o rozbiciu na bajty!):

0x12345678 → 12 34 56 78

Możliwość 3:
Dla "ułatwienia" ktoś jeszcze wymyślił, że można zapisać wordy wewnętrznie LE a potem wordy w dwordzie BE (przyjeło się, że word to 16-bitów, czyli 2 bajty, chociaż nie jest to w pełni poprawne, szczególnie na architekturach na których "słowo maszynowe" (machine word) ma np. 64-bity), np.:

0x12345678 → 34 12 78 56

Lub odwrotnie! Wordy wewnętrznie BE a zew. LE:

0x12345678 → 56 78 12 34

Powyższa mieszanka nosi nazwę Mixed Endian lub Middle Endian (jest to ogólny termin).

Wartość, kodowanie i zapis w pamięci w C/C++

C/C++ jest o tyle fajnym językiem, że można w nim operować zarówno na poziomie wartości, jak i "mieszać" bezpośrednio na zapisanej w pamięci wersji zakodowanej zmiennej.
Żeby to osiągnąć, należy dobrać się do zapisu bajtowego zmiennej, zakodowanego w naturalnym binarnym (ponieważ jest on najprostszy i najbliższy zapisowi fizycznemu) - taak, chodzi o unsigned char (ew. uint8_t jesli ktoś lubi stdint.h).

Załóżmy więc, że mamy zmienną float:
float f = 1234.5678f;

I teraz, możemy zrobić dwie rzeczy:

Opcja 1:
Posłużyć się union'em (czyli skorzystać z tego, że dwa rodzaje zmiennych mogą być zapisane w tym samym miejscu w pamięci) - jest to wersja dla osób które jeszcze nie poznały wskaźników (lub się z nimi nie lubią)

float f = 1234.5678f;
union {
 float f;
 unsigned char ch[4]; // float ma 32 bity, czyli 4 bajty po 8 bitow
 unsigned int i; // zeby wypisac po konwersji z LE do postaci 32-bitowej
} internal_f;
internal_f.f = f;
printf("W pamieci (LE): %.2x %.2x %.2x %.2x, Zakodowana: %.8x, Wartosc: %f\n",
 internal_f.ch[0], internal_f.ch[1], internal_f.ch[2], internal_f.ch[3],
 internal_f.i, internal_f.f);
Wynik działania:
W pamieci (LE): 2b 52 9a 44, Zakodowana: 449a522b, Wartosc: 1234.567749

Zauważmy trzy rzeczy:
1. Skorzystaliśmy z faktu, że odczyt unsigned int'a jest równoznaczny z konwersją LE do 32-bitowej wartości.
2. Wypisana wartość jest inna niż zapisana w kodzie - najwyraźniej wartości 1234.5678 nie ma w zbiorze możliwych wartości dla floatów.
3. printf to świetne narzędzie do reprezentacji wartości w rożnej postaci (polecam się dobrze zapoznać z tą funkcją)

Opcja 2:
Drugą opcją, bardziej wygodną, jest skorzystanie ze wskaźników:

float f = 1234.5678f;
unsigned char *ch = (unsigned char*)&f;
unsigned int *i = (unsigned int*)&f;
printf("W pamieci (LE): %.2x %.2x %.2x %.2x, Zakodowana: %.8x, Wartosc: %f\n",
 ch[0], ch[1], ch[2], ch[3], *i, f);
Wynik (taki sam):
W pamieci (LE): 2b 52 9a 44, Zakodowana: 449a522b, Wartosc: 1234.567749

Uwaga: (dot. linii zaznaczonej na żółto) w tym miejscu odwołuje się do float'a korzystając ze wskaźnika na unsigned int - jest to niezgodne z tzw. zasadą strict-aliasing'u i może wywołać problemy w przypadku bardzo agresywnej optymalizacji. Warto rzucić okiem w dokumentacji kompilatora na opcje informujące kompilator o niestosowaniu tej zasady w kodzie (patrz -fno-strict-aliasing w GCC). W normalnych projektach powinno się unikać łamania tej zasady, jednak pisząc kod dla siebie można czasem przymknąć na nią oko ;)
Zasady strict aliasingu nie łamie natomiast używanie korzystanie z odwołania do zmiennej per bajt. Używanie union (jeśli zawiera oba używane typy) również jest OK. Więcej info można znaleźć np. w standardzie C99 punkt 6.5/7.
[Podziękowanie dla Fanaela za zwrócenia uwagi na powyższy problem]

Oczywiście, możemy też zrobić to w drugą stronę, np. weźmy te zakodowane bajty i wypiszmy je jako float, np.:

unsigned char ch[4] = { 0x2b, 0x52, 0x9a, 0x44 };
float f = *(float*)ch;
printf("%f\n", f);
Lub, jeśli nie chcemy się z LE bawić:

unsigned int i = 0x449a522b;
float f = *(float*)&i;
printf("%f\n", f);
Możemy też trochę "zaszaleć" i użyć c-stringu jako "nośnika danych" (przypominam o LE!) - w końcu c-string to po prostu seria bajtów zapisana w pamięci, a zapis z cudzysłowiem w C/C++ (np. "asdf") to de facto ulokowanie w pamięci (zazwyczaj tylko do odczytu) ciągu ['a', 's', 'd', 'f', 0] oraz zwrócenie jego adresu (wskaźnika na niego) (taak, "asdf" to pointer):

float f = *(float*)"\x2b\x52\x9a\x44";
printf("%f\n", f);

Podsumowanie

Rozróżnianie reprezentacji od wartości od znaczenia logicznego zmiennej jest obowiązkowe dla każdego programisty. Dodatkowo, dobry programista powinien znać przynajmniej podstawy kodowania zmiennych oraz ich zapisu w pamięci dla jezyka z którego korzysta.
Dla reverserów i osób zajmujących się low-level security cały powyższy materiał jest obowiązkowy :)

Na koniec jeszcze jeden pełny przykład opisu zmiennej w programie:

#include <stdio.h>
int main(void)
{
 int i;
 puts("ile masz lat?"); scanf("%i", &i);
 printf("masz %i lat (czyli %x w hexa)\n", i, i);
 return 0;
}
W powyższym programie:
- użytkownik może wprowadzić wartość (scanf) reprezentując ją w systemie dziesiętnym (np. 123), ósemkowym (np. 0123) lub szesnastkowym (0x123) (tak działa %i w scanf, w przeciwieństwie do %d które oczekuje zawsze reprezentacji dziesiętnej)
- wartość jest przechowywana w zmiennej o typie int, kodowanym w ZU2 o wielkości 32-bitów
- zmienna i jest zapisana LE w pamięci
- na poziomie logiki zmienna i przechowuje wiek
- na koniec zmienna jest wypisywana (printf) w reprezentacji dziesiętnej (%i) oraz hexadecymalnej (%x)

Całkiem sporo info jak na jedną zmienną :)

Co dalej...

Zainteresowanych zachęcam do pobawienia się różnymi kodowniami które wymieniłem wcześniej, zarówno tymi "natywnymi", jak i emulowanymi (np. typy fixed point w GCC).
Warto również, w ramach ćwiczeń, wybrać jakieś kodowanie (np. fixed point) i zrobić sobie zestaw funkcji/struktur/klas do operacji na nim.
Świetnym ćwiczeniem jest również napisanie kilku funkcji do konwersji wartość->reprezentacja oraz reprezentacja->wartość, np. dla U2 oraz natywnego binarnego (oraz IEEE-754 dla bardzo ambitnych).

Poza tym, artykuł napomknął tylko o kodowaniu ciągów (tekstu) - jest to temat morze, bardzo ciekawy i również obowiązkowy dla programistow i osób zajmujących się bezpieczeństwem. Jest kilka bardzo ciekawych kodowań tekstu, takich jak np. UTF-8, UTF-16, UTC-2, UTF-7 (zmora security) czy np. Punycode. Warto się po nich rozejrzeć. Do tego dochodzi jeszcze zapis "struktury" tekstu w pamięci, czyli podejście z terminatorem (np. C string lub stringi w DOSie) vs podejście z zapisaną długością ciągu (jak np. w Javie czy PHP).

Warto rzucić również okiem na assembly różnych procesorów i natywne kodowania zmiennych które obsługują (np. x86 obsługuje natywny binarny, ZU2, IEEE-754 i BCD) - assembly jest o tyle ciekawy, że do różnych kodowań są różne instrukcje (np. DIV do natywnego binarnego vs IDIV do ZU2 vs FDIV do IEEE-754). Również dedykowane instrukcje do obsługi ciągów tekstu są interesujące, np. dodane w Pentium instrukcje REP(E/NE) SCAS/etc lub dodane w SSE 4.2 PCMPxSTRx.

Gynvael Coldwind
team Vexillium
http://gynvael.coldwind.pl

Notka na temat kopiowania postu "Zmienne i stałe: wartość, kodowanie, reprezentacja": Niniejszym udzielam zgody na kopiowanie, rozpowszechnianie i publikowanie niniejszego artykułu, pod warunkiem iż forma i treść pozostanie niezmieniona, prawdziwy autor jasno określony, a artykuł będzie prezentowany nieodpłatnie, w pełnej postaci. W przypadku wątpliwości można się ze mną skontaktować, nie gryzę ;>